ウォリスの公式
命題
次の等式が成り立つ。
別の形式
この式は次のように書くこともできる。
左辺を因数分解すると、
二重階乗を使うと、
逆数を取ると、
二重階乗の形式を変形すると、
両辺の平方根を取って、
左辺に
この形式も非常によく使われる。
さらに、
という漸近があるという風にも読める。
正弦関数の因数分解による証明
バーゼル問題 でみたが、正弦関数は形式的に次のように因数分解される。
両辺に
を得る。
ウォリス積分による証明
ウォリス積分と呼ばれる以下の積分を利用した証明方法もあり、これも面白い。
被積分関数
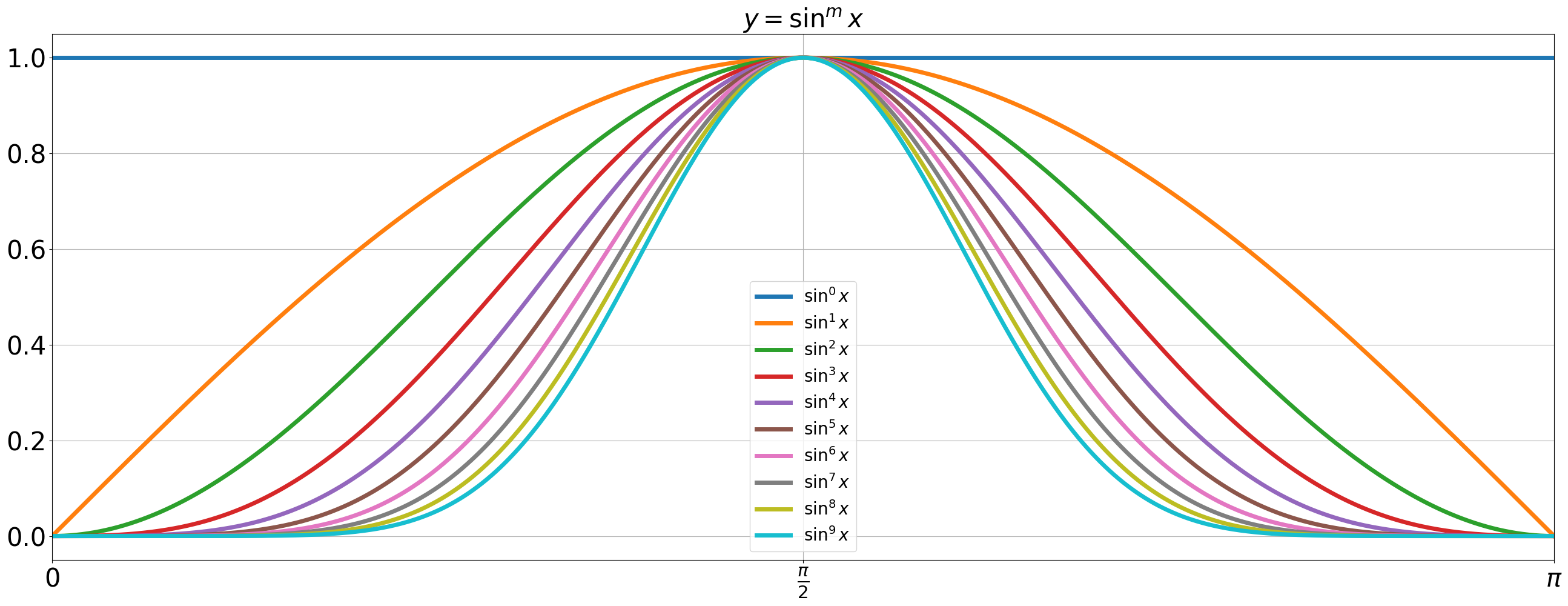
ウォリス積分は、このグラフと
後で見るが、ウォリス積分からウォリスの公式を導く際には、この面積自体ではなく、
なお、
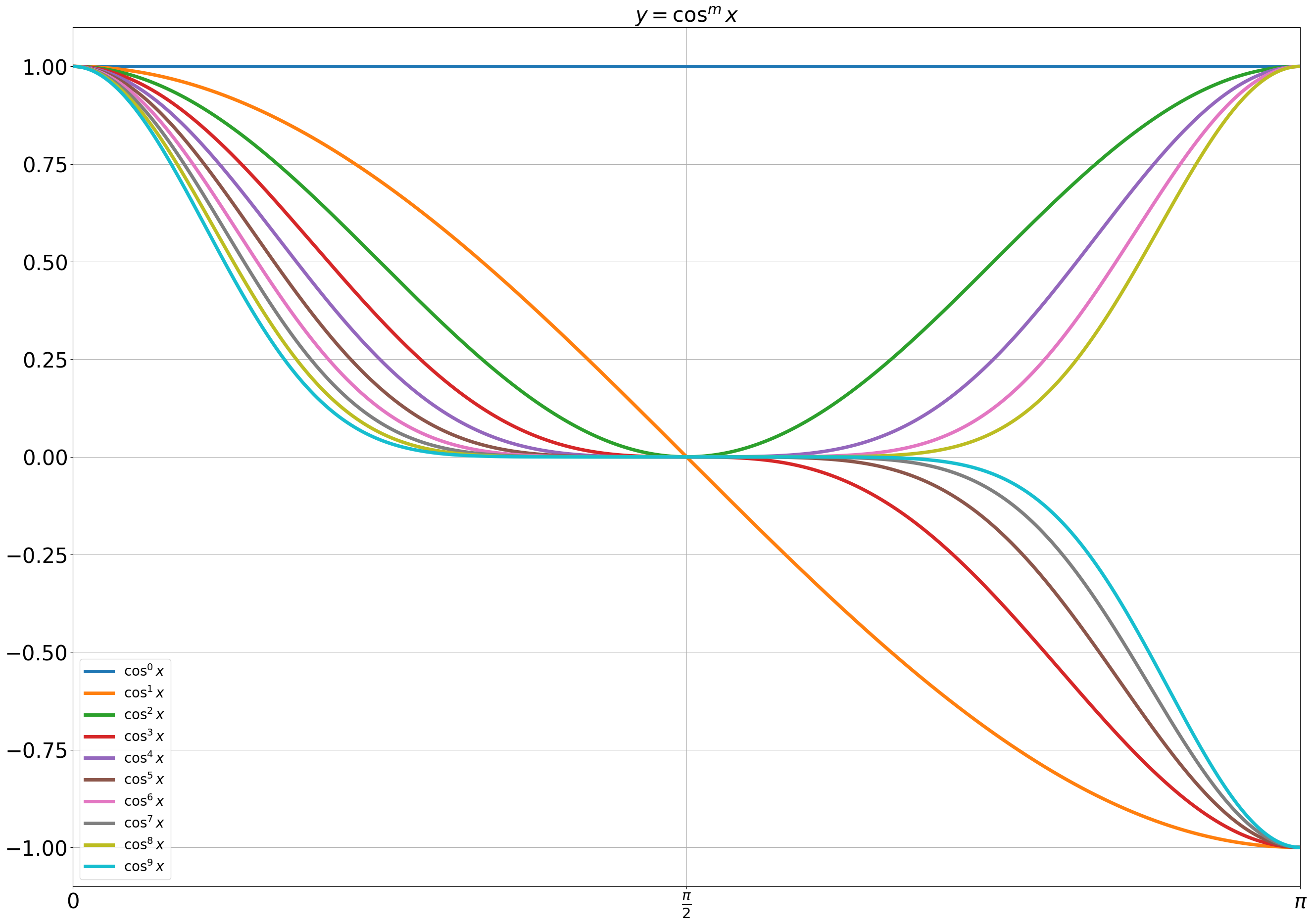
区間
として定義してもよい。
さて、部分積分により、
という漸化式が得られる。
に注意して、
となる。
一方、
各辺を
よって、
すなわち、隣り合う項の比は
なので、結局、
となり、ウォリスの公式が得られた。
ウォリス積分の漸近
さて、もう少しウォリス積分について調べよう。隣り合う項の積を考える。
漸化式
より、
これを繰り返し用いると、結局、
先の結果から、
すなわち、
となり、
がわかる。
ウォリス積分をグラフに表すと次のようになる。

補足
ウォリスの公式は、
スターリングの公式という階乗(もしくはガンマ関数)の近似公式の証明に使われることがある。
また、ガウス積分を求めるのにも利用され、意外といろいろな応用がある公式である。