ウォリス積分を用いたガウス積分の証明
命題
次が成り立つ。
証明
補題
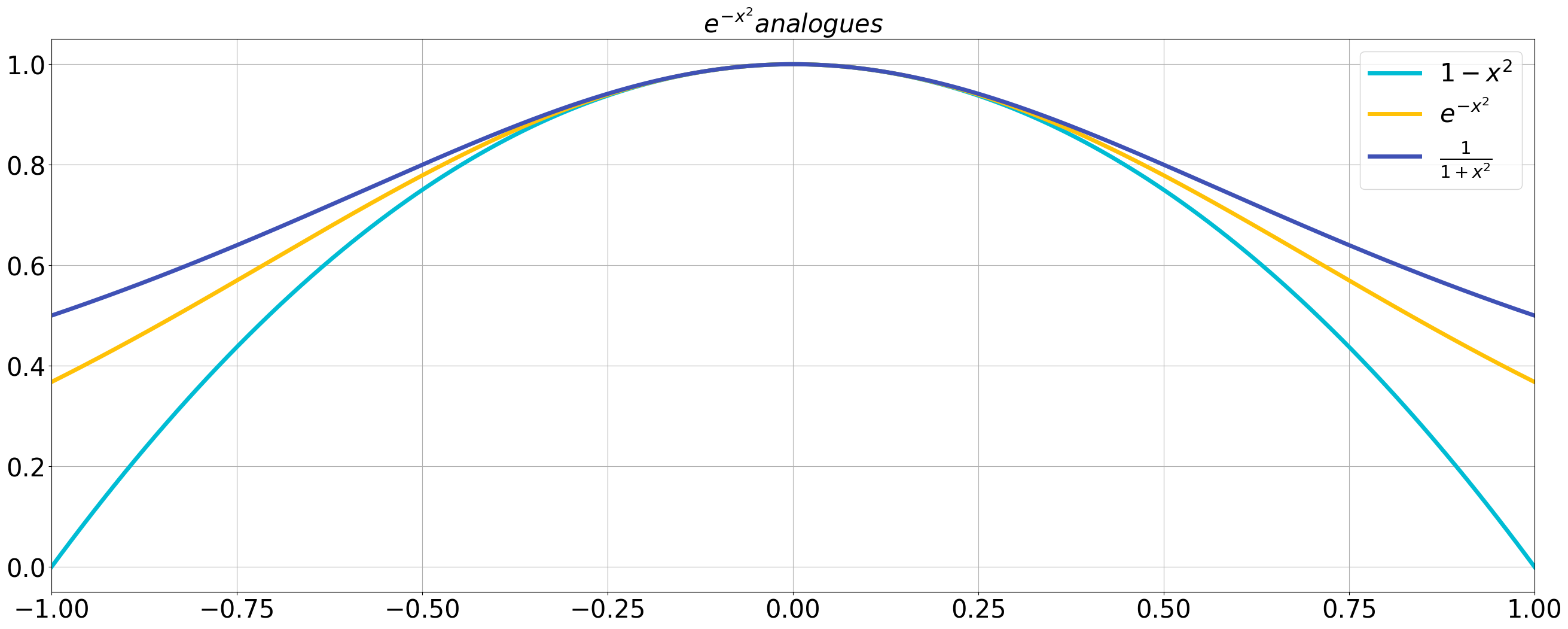
補題の証明
である。
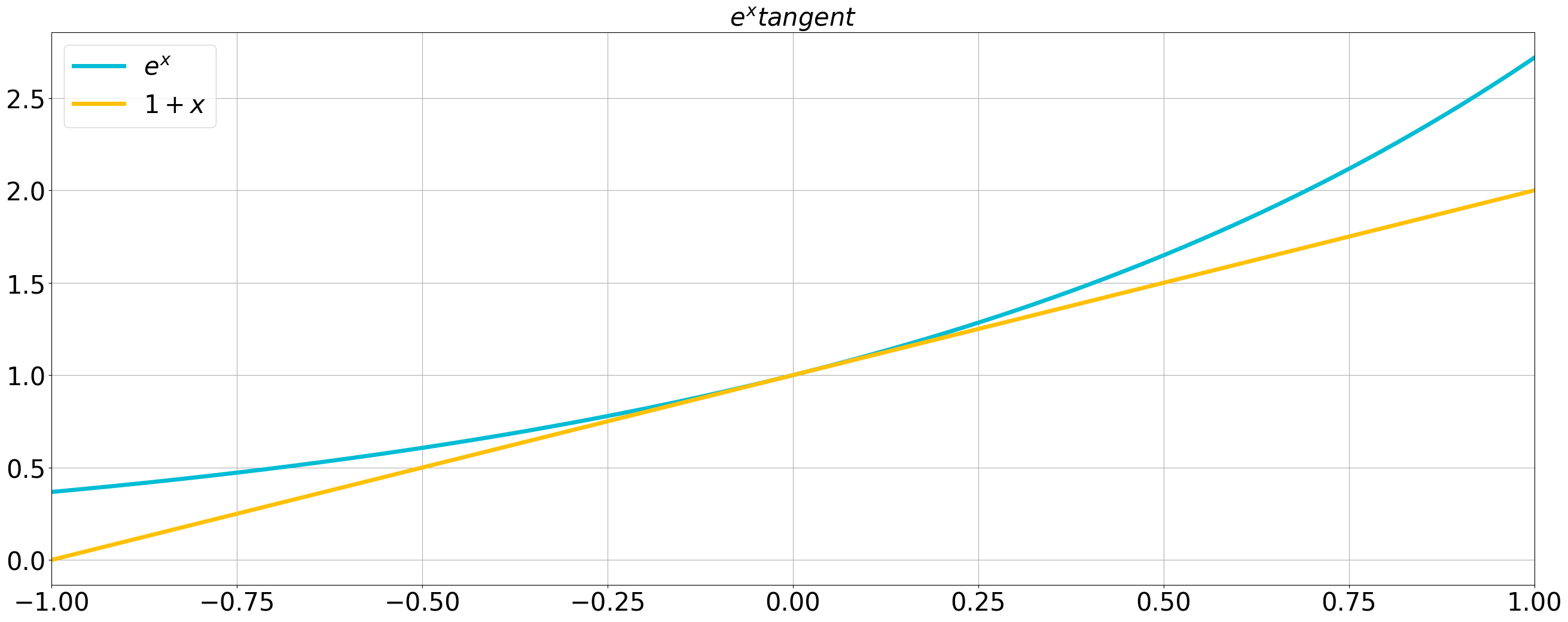
実際、右辺は左辺のテイラー展開の2次以降を打ち切った形であり、すなわち、
したがって、
この不等式の
また、
ウォリス積分の置換
ウォリス積分
を考える。
ガウス積分の評価
とおく。
補題から、
最右辺と最左辺はウォリス積分を置換積分したのと同じ形であるから、結局、
である。
ウォリスの公式 で見たように、
なので、
よって、
積分区間の調整
被積分関数は偶関数であるから、
よって示された。