集合の極限

March 13, 2021

数列の極限

実数列 ${a_{n}}$ が、ある実数 $α$ に収束する、とは次の意味であった。

$\forall ϵ > 0; \exists N \in N s.t. n > N ⟹ | a_{n} - α | < ϵ$

これから集合列に対する極限を考えていくが、この定義を直接応用するのは難しい。集合と集合の差が $ϵ$ 未満とはどういう意味なのかわからないからである。

集合の単調増大列 / 単調減少列の極限

とはいえ、任意の集合列の極限の定義は置いておくにしても、次のような列についての極限を考えるのは比較的容易いだろう。

単調増大列

集合列 ${A_{n}}$ は任意の $n$ に対して、 $A_{n} \subset A_{n + 1}$ を充たすとする。すなわち、 $A_{1} \subset A_{2} \subset A_{3} \subset A_{4} \subset \dots$ このとき、集合列 ${A_{n}}$ は単調増大列であるという。

このとき、

$lim_{n \to \infty} A_{n} = ⋃_{n = 1}^{\infty} A_{n}$

と定める。

右辺にも $\infty$ が出てきていて、どういう定義なのかわかりづらいが、右辺の意味は「少なくとも一つの $n$ があって、 $A_{n}$ の元となるような要素をすべて集めたもの」であり、実は極限的な意味は何もない。

きちんと記号でかけば、

$⋃_{n = 1}^{\infty} A_{n} = {x | \exists n \in N; x \in A_{n}}$

ということであり、任意の集合列に対して定義できるものである。

単調減少列

集合列 ${A_{n}}$ は任意の $n$ に対して、 $A_{n} \supset A_{n + 1}$ を充たすとする。すなわち、 $A_{1} \supset A_{2} \supset A_{3} \supset A_{4} \supset \dots$ このとき、集合列 ${A_{n}}$ は単調減少列であるという。

このとき、

$lim_{n \to \infty} A_{n} = ⋂_{n = 1}^{\infty} A_{n}$

と定める。

右辺の意味は「すべての $A_{n}$ の元となるような要素をすべて集めたもの」である。

きちんと記号でかけば、

$⋂_{n = 1}^{\infty} A_{n} = {x | \forall n \in N; x \in A_{n}}$

ということであり、任意の集合列に対して定義できるものである。

数列の単調列

ここで証明はしないが、次の定理がある。

実数列の単調増大列は、有界ならその上限に収束し、非有界なら $\infty$ に発散する。
実数列の単調減少列は、有界ならその下限に収束し、非有界なら $- \infty$ に発散する。

この定理と、上で定義した集合の単調列の極限の定義を比較すると、 $⋃$ は上限のようなもの、 $⋂$ は下限のようなものであると類推できる。

単調列以外の集合列の極限を定義するにあたっては、こういった概念を敷衍すればよいわけである。

数列の上極限・下極限

そこで、次のような概念を思い出す。

数列 ${a_{n}}$ に対して、その上極限を次で定める。

$\underset{n \to \infty}{lim sup} a_{n} = inf_{n \in N} sup_{k \geq n} a_{k}$

下極限を次で定める。

$\underset{n \to \infty}{lim inf} a_{n} = sup_{n \in N} inf_{k \geq n} a_{k}$

上極限・下極限は、任意の数列に対して定義できるという、強い性質を持つ。

また、次の定理がある。

実数列の上極限と下極限が一致するなら、実数列は極限( $\infty$ 、 $- \infty$ を含む)を持つ。極限の値は上極限(=下極限)と一致する。逆に、実数列が極限を持つならば、上極限と下極限は極限に一致する。

この定理を利用すると、単調でない集合列にも極限が定義できるだろう。

上極限・下極限は、上限・下限さえ知っていれば定義でき、先の考察で $⋃$ が上限のようなもの、 $⋂$ が下限のようなものであるということは分かっているからである。

集合列の上極限・下極限・極限

集合列 ${A_{n}}$ に対して、その上極限、下極限を次のように定める。

$\underset{n \to \infty}{lim sup} A_{n} = ⋂_{n = 1}^{\infty} ⋃_{k = n}^{\infty} A_{k}$

$\underset{n \to \infty}{lim inf} A_{n} = ⋃_{n = 1}^{\infty} ⋂_{k = n}^{\infty} A_{k}$

もし、

$\underset{n \to \infty}{lim sup} A_{n} = \underset{n \to \infty}{lim inf} A_{n}$

が成り立つなら、これを集合列 ${A_{n}}$ の極限といい、

$lim_{n \to \infty} A_{n}$

で表す。

集合列の極限が存在しない例

上で集合列の極限は定義されたが、イメージがつかみにくいかもしれないので例を挙げる。

実はこの例では、極限が存在しないことが示されてしまうのだが、エッジケースであり、イメージを掴むのには十分であると思う。

集合列 ${X_{n}}$ を次で定める。

$X_{n} = {x \in R | - 1 - \frac{(- 1)^{n}}{n} \leq x \leq 1 + \frac{(- 1)^{n}}{n}}$

最初の4項を示すと、以下の通りである。

$X_{1} = [0, 0]$

$X_{2} = [- \frac{3}{2}, \frac{3}{2}]$

$X_{3} = [- \frac{2}{3}, \frac{2}{3}]$

$X_{4} = [- \frac{5}{4}, \frac{5}{4}]$

グラフにすると、以下の通りである。

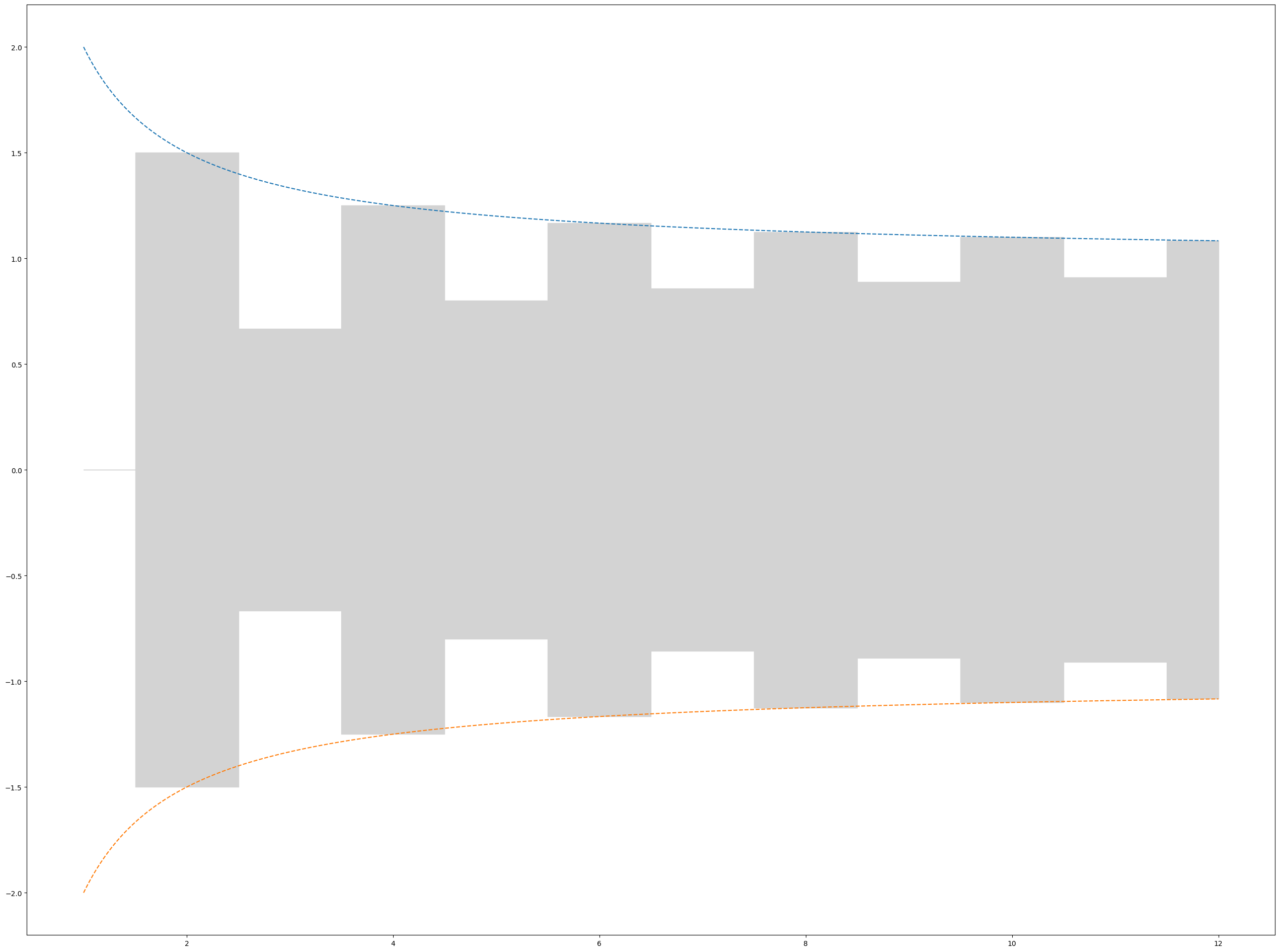
グラフからは、 ${X_{n}}$ は単調でないが、ゆっくりと $[- 1, 1]$ に収束していくように見える。

しかし、定義に従って正確に議論すると、実は違うことがわかる。

それを以下で示そう。

$n$ が偶数のとき、 $⋃_{k = n}^{\infty} X_{k} = X_{n}$ となる。

これは、 ${X_{n}}$ の偶数番目だけを取った部分列が単調減少列であり、 $X_{2 n} \supset [- 1, 1] \supset X_{2 m + 1}$ が任意の $n, m$ に対して成立することからわかる。

同様の考察で、

$n$ が奇数のとき、 $⋃_{k = n}^{\infty} X_{k} = X_{n + 1}$

$n$ が偶数のとき、 $⋂_{k = n}^{\infty} X_{k} = X_{n + 1}$

$n$ が奇数のとき、 $⋂_{k = n}^{\infty} X_{k} = X_{n}$

がわかる。したがって、

$\underset{n \to \infty}{lim sup} X_{n} = ⋂_{n = 1}^{\infty} X_{2 n} = [- 1, 1]$

$\underset{n \to \infty}{lim inf} X_{n} = ⋃_{n = 1}^{\infty} X_{2 n + 1} = (- 1, 1)$

ゆえに、

$\underset{n \to \infty}{lim sup} X_{n} \neq \underset{n \to \infty}{lim inf} X_{n}$

であり、極限は存在しないことがわかる。

大変惜しい。

集合列の極限が存在する例

上の例を少し変形して、

$X_{n} = {x \in R | - 1 - \frac{(- 1)^{n}}{n} \leq x \leq 1 + \frac{(- 1)^{n}}{n}} - {- 1, 1}$

などとすると、

$\underset{n \to \infty}{lim sup} X_{n} = \underset{n \to \infty}{lim inf} X_{n} = (- 1, 1)$

となり、極限が定義できるようになる。

ただ、これは些か不便であり、位相を仮定せず一般の集合列に対して、極限を定義した点に問題があると思う。

たとえば、位相空間の部分集合列で、上極限と下極限が集積点の違いを除いて一致するなら、その間の何かや、閉包、開核を以て「極限のようなもの」を定義しても良いとは思う。

ただし、多くの文献で、集合列の極限は測度論の文脈で語られているため、こういった点に言及しているものはなく、一般的なアイデアではないかもしれない。

位相空間については、部分集合列の極限を考えるよりも、点列の極限を考えることができれば、それで十分という場合が多いのかもしれない。

集合列の上極限・下極限の言い換え

まだイメージが掴みづらい読者のために、より簡潔な言い換えを紹介しておく。

「 $x$ が集合列 ${A_{n}}$ の上極限に含まれる」とは、 $| {A_{n} | x \in A_{n}} | = ℵ_{0}$ の意味である。

「 $x$ が集合列 ${A_{n}}$ の下極限に含まれる」とは、 $| {A_{n} | x \notin A_{n}} | < ℵ_{0}$ の意味である。

この言い換えから明らかなように、下極限は必ず上極限の部分集合になる。

集合列に極限が存在するのは、「 $x$ を含む項が無限に存在するなら、 $x$ を含まないような項は高々有限個になる」という条件が成り立つ場合である。

またいいかえれば、「任意の $x$ に対して、 $x$ を含む項が無限個ある、または、 $x$ を含まない項が無限個ある、のいずれか一方のみが成り立つ」ような場合である。

一般的な集合列の極限の定義が、単調列の場合の定義とcompatibleであることの証明

まず集合列が単調列の場合に極限を定義し、次に一般的な場合を考えた。

これらの定義が一致することの証明をここで与える。

集合列 ${A_{n}}$ は単調増大列とする。

このとき、任意の $n$ について

$⋃_{k = n}^{\infty} A_{k} = ⋃_{k = 1}^{\infty} A_{k}$

がわかる。実際、

$⋃_{k = 1}^{\infty} A_{k} = (⋃_{k = 1}^{n} A_{k}) \cup (⋃_{k = n}^{\infty} A_{k}) = A_{n} \cup (⋃_{k = n}^{\infty} A_{k}) = ⋃_{k = n}^{\infty} A_{k}$

したがって、

$\underset{n \to \infty}{lim sup} A_{n} = ⋂_{n = 1}^{\infty} ⋃_{k = n}^{\infty} A_{k} = ⋃_{k = 1}^{\infty} A_{k}$

また、単調増大性から、

$⋂_{k = n}^{\infty} A_{k} = A_{n}$

であり、ゆえに

$\underset{n \to \infty}{lim inf} A_{n} = ⋃_{n = 1}^{\infty} ⋂_{k = n}^{\infty} A_{k} = ⋃_{n = 1}^{\infty} A_{n}$

がわかる。

よって、上極限と下極限が一致するため、一般的な定義においても極限が存在し、それは単調増大列に対して定義した極限 $⋃_{n = 1}^{\infty} A_{n}$ と一致する。

単調減少列に対する極限も、同様の議論で一致することがわかる。