フレネル積分

September 6, 2024

フレネル積分とはなにか？

フレネル積分(Fresnel integrals)とは、次の積分によって表される2つの関数である。

$S (x) = \int_{0}^{x} \sin (t^{2}) d t$

$C (x) = \int_{0}^{x} \cos (t^{2}) d t$

変数の定数倍の違いであるが、次の定義も使われる。

$S (x) = \int_{0}^{x} \sin (\frac{π}{2} t^{2}) d t$

$C (x) = \int_{0}^{x} \cos (\frac{π}{2} t^{2}) d t$

$\sin (x^{2})$ と $\cos (x^{2})$ のグラフ

まず、それぞれの被積分関数である $\sin (x^{2})$ と $\cos (x^{2})$ の様子を確認しておこう。

いずれも偶関数であり、0付近では緩やかな様子だが、両端に近づくにつれて振動が激しくなる (周期が短くなる) 事がわかる。

$S (x)$ と $C (x)$ のグラフ

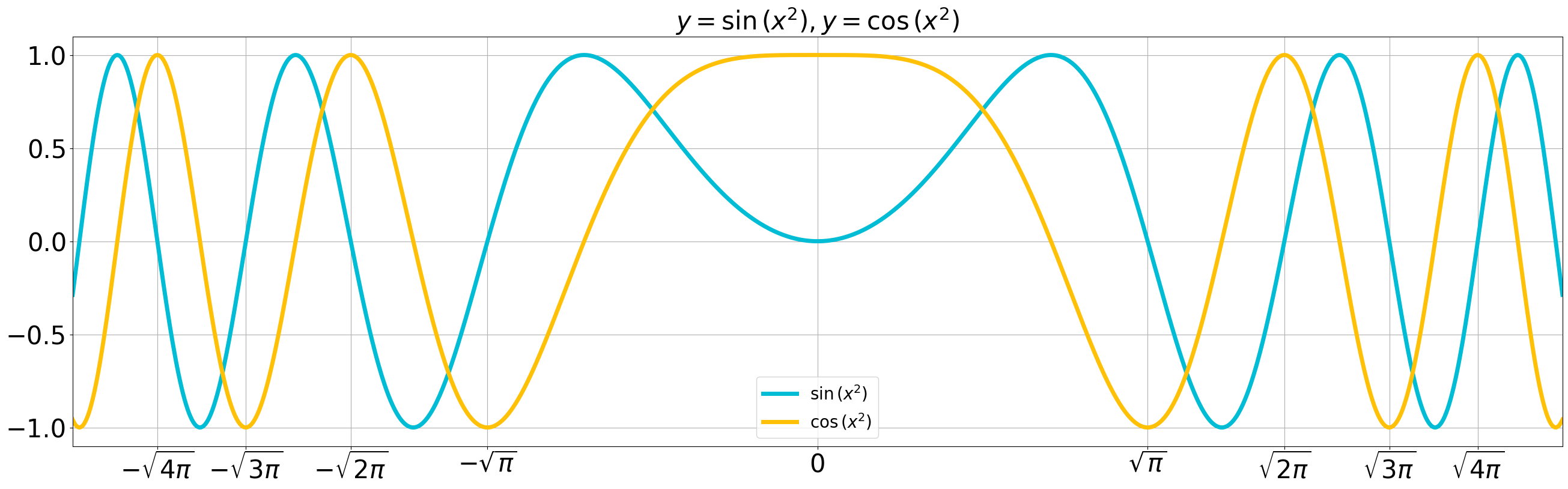
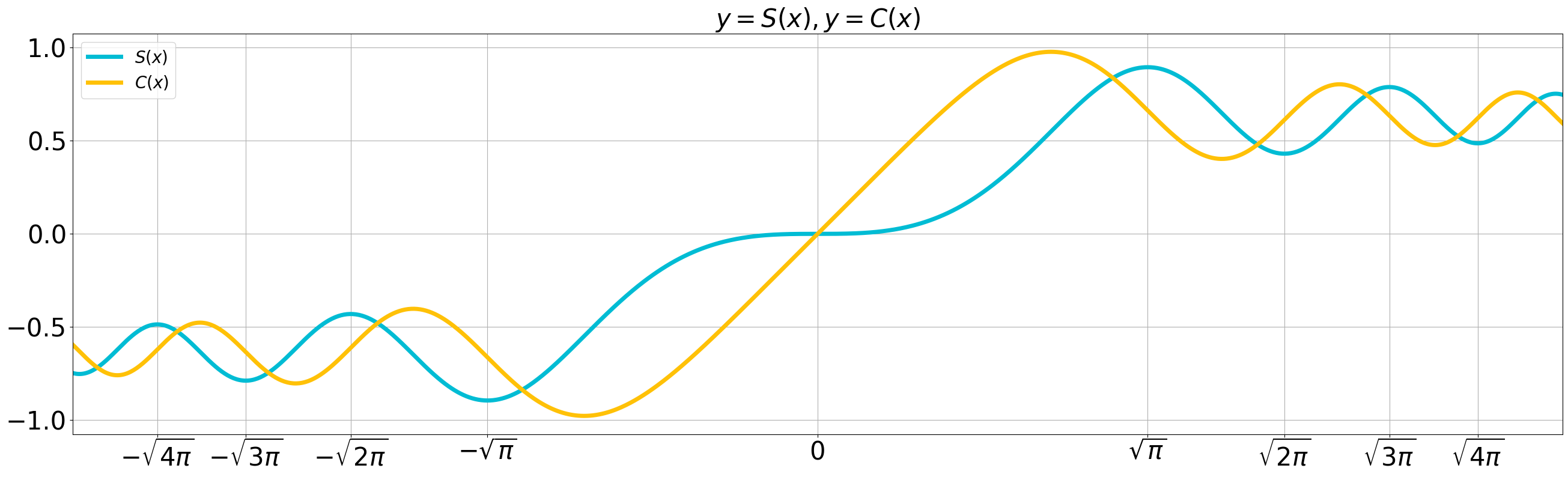
次に、フレネル積分の様子をグラフで確認する。

いずれも奇関数であり、有界である。

両端では振動しているが、その振動具合は少しずつ小さくなっており、 $x \to \infty$ において収束すると考えられる。

$(C (t), S (t))$ のグラフ

$x = C (t), y = S (t)$ としたときの軌跡もグラフで確認しておこう。

$t \to \pm \infty$ において、無限回回転しながら、一点に収束すると考えられる。

この軌跡はオイラー螺旋(Euler spiral)と呼ばれ、またクロソイド(clothoid)もしくは、コルニュ螺旋(Cornu spiral)とも呼ばれる。

ギリシャ神話で糸巻き棒のシンボルで表される女神クロートーに因んでクロソイドという名を付けたのは、チェザロである。

SciPyにおけるフレネル積分

上の図は、SciPyライブラリのscipy.special.fresnelを用いて描画した。

この関数は、冒頭に述べた2番目の定義を実装している。

https://docs.scipy.org/doc/scipy/reference/generated/scipy.special.fresnel.html

上の図は適当な変換をして描画したものである。

フレネル積分の極限

図が示唆するように、フレネル積分は $x \to \infty$ において収束する。この極限を求めよう。

$\int_{0}^{\infty} \sin (t^{2}) d t$

$\int_{0}^{\infty} \cos (t^{2}) d t$

を個別に求める代わりに、

$\int_{0}^{\infty} {\cos (t^{2}) + i \sin (t^{2})} d t = \int_{0}^{\infty} e^{i t^{2}} d t$

を考える。

教科書的な解法

$R$ を正の実数として、次のような積分路を考える。

$C_{1} : 0 \to R$

$C_{2} : R \to R \exp [\frac{π}{4} i]$

$C_{3} : R \exp [\frac{π}{4} i] \to 0$

$C = C_{1} + C_{2} + C_{3}$

ここで、 $C_{1}$ は実軸上を直線的に進み、 $C_{2}$ は8分の1回転を円周状に進む経路であり、 $C_{3}$ はそこから原点に直線的に戻る経路である。

また、各経路に沿った $e^{i z^{2}}$ の複素積分をそれぞれ、 $I_{1}$ , $I_{2}$ , $I_{3}$ とする。求めたいのは $I_{1}$ の $R \to \infty$ における極限である。

さて、 $e^{i z^{2}}$ は正則であり、 $C$ は複素平面上の単純閉曲線であるから、Cauchyの積分定理により、

$I = I_{1} + I_{2} + I_{3} = 0$

である。 $I_{2}$ および、 $I_{3}$ を計算しよう。結論を先に述べると、 $I_{2}$ は $0$ に収束し、 $I_{3}$ はガウス積分となる。

$I_{2} = \int_{C_{2}} e^{i z^{2}} d z = \int_{θ = 0}^{\frac{π}{4}} \exp [i (R e^{i θ})^{2}] \cdot i R e^{i θ} d θ$

$| I_{2} | \leq \int_{θ = 0}^{\frac{π}{4}} | \exp [i (R e^{i θ})^{2}] \cdot i R e^{i θ} | d θ = R \int_{θ = 0}^{\frac{π}{4}} | \exp [i (R e^{i θ})^{2}] | d θ = R \int_{θ = 0}^{\frac{π}{4}} \exp [ℜ (i (R e^{i θ})^{2})] d θ = R \int_{θ = 0}^{\frac{π}{4}} \exp [- R^{2} \sin 2 θ] d θ$

右辺の積分区間において、 $\sin 2 θ$ は上に凸であり、したがって

$\sin 2 θ \geq \frac{4}{π} θ$

が成り立つ。そこで、

$| I_{2} | \leq R \int_{θ = 0}^{\frac{π}{4}} \exp [- R^{2} \sin 2 θ] d θ \leq R \int_{θ = 0}^{\frac{π}{4}} \exp [- R^{2} \frac{4}{π} θ] d θ = R {[- \frac{π}{4 R^{2}} \exp [- \frac{4 R^{2}}{π} θ]]}_{0}^{\frac{π}{4}} = \frac{π}{4} \frac{1 - \exp [- R^{2}]}{R}$

となるが、右辺は $R \to \infty$ において $0$ に収束する。

したがって、 $I_{2} \to 0$ である。

次に、

$I_{3} = \int_{C_{3}} e^{i z^{2}} d z = \int_{r = R}^{0} \exp [i (r e^{i \frac{π}{4}})^{2}] \cdot e^{i \frac{π}{4}} d r = - \int_{r = 0}^{R} \exp [i (r^{2} e^{i \frac{π}{2}})] \cdot (\frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}} i) d r = - (\frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}} i) \int_{r = 0}^{R} \exp [- r^{2}] d r$

となり、右辺はガウス積分であるから、 $R \to \infty$ において

$I_{3} \to - (\frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}} i) \frac{\sqrt{π}}{2}$

に収束する。

以上をまとめると、

$I = I_{1} + I_{2} + I_{3} = 0$

$I_{2} \to 0$

$I_{3} \to - (\frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}} i) \frac{\sqrt{π}}{2}$

したがって、

$I_{1} \to (\frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}} i) \frac{\sqrt{π}}{2} = \int_{0}^{\infty} {\cos (t^{2}) + i \sin (t^{2})} d t$

両辺の実部と虚部を比較して、

$lim_{x \to \infty} S (x) = \int_{0}^{\infty} \sin (t^{2}) d t = \frac{1}{2} \sqrt{\frac{π}{2}}$

$lim_{x \to \infty} C (x) = \int_{0}^{\infty} \cos (t^{2}) d t = \frac{1}{2} \sqrt{\frac{π}{2}}$

これはおおよそ、0.626657という値である。

先のオイラー螺旋のグラフを改めて見返すと、実際、最終的にその辺りの値に収束しそうである。

変数変換による方法

上はよく教科書に載っているが、積分路がやや唐突であるのは否めないので、こういった積分路が出てくる事情をもうすこし考えてみよう。

求めたい積分

$\int_{0}^{\infty} e^{i t^{2}} d t$

と、既に知っているガウス積分

$\int_{0}^{\infty} e^{- t^{2}} d t = \frac{\sqrt{π}}{2}$

は非常によく似ているので、「変数変換によってガウス積分に帰着できそうである」と考える。

そこで次のように変形する。

$\int_{0}^{\infty} e^{i t^{2}} d t = \int_{0}^{\infty} \exp [i t^{2}] d t = \int_{0}^{\infty} \exp [(- 1) (- i) t^{2}] d t = \int_{0}^{\infty} \exp [- e^{- \frac{π}{2} i} t^{2}] d t = \int_{0}^{\infty} \exp [- (e^{- \frac{π}{4} i} t)^{2}] d t$

そこで、変数変換 $s = e^{- \frac{π}{4} i} t$ を考えると、

$\int_{0}^{\infty} e^{i t^{2}} d t = \int_{0}^{e^{- \frac{π}{4} i} \infty} \exp [- s^{2}] e^{\frac{π}{4} i} d s = e^{\frac{π}{4} i} \int_{0}^{e^{- \frac{π}{4} i} \infty} \exp [- s^{2}] d s$

となり、複素平面を右下に向かう積分路の広義積分が現れる。

これを求めるために、先ほどと同じように扇形を一周するような積分路でガウス積分を考えてやると、 8分の1回転の部分は0に収束するので結局実軸上でガウス積分をしているのと同じことだとわかる。

そこで、

$\int_{0}^{\infty} e^{i t^{2}} d t = e^{\frac{π}{4} i} \int_{0}^{e^{- \frac{π}{4} i} \infty} \exp [- s^{2}] d s = e^{\frac{π}{4} i} \frac{\sqrt{π}}{2} = (\frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}} i) \frac{\sqrt{π}}{2}$

と積分が求まる。

先に述べた方法で8分の1回転の積分路が出てくる事情はこのようなところにある。

オイラー螺旋の弧長

オイラー螺旋

$(x, y) = (C (t), S (t))$

の速度ベクトルは、

$(\dot{x}, \dot{y}) = (\cos (t^{2}), \sin (t^{2}))$

である。これの大きさは1であるから、オイラー螺旋は、単位時間あたりに1だけ進むと考えられる。

したがって、時刻 $0$ からのオイラー螺旋の弧長は

$L = t$

である。

オイラー螺旋の曲率

また、加速度ベクトルは、

$(\ddot{x}, \ddot{y}) = (- 2 t \sin (t^{2}), 2 t \cos (t^{2}))$

なので、曲率半径は、

$R = \frac{({\dot{x}}^{2} + {\dot{y}}^{2})^{\frac{3}{2}}}{\dot{x} \ddot{y} - \dot{y} \ddot{x}} = \frac{1}{2 t}$

曲率は、

$κ = \frac{1}{R} = 2 t$

である。

補足

フレネル積分の極限は、少しテクニカルな方法で求めた。ポイントはガウス積分を見越して8分の1回転の積分路を作るところである。もう少し別の方法としては、メリン変換(Mellin transform)による方法がある。

オイラー螺旋には、弧長と曲率に比例関係があるという面白い性質がある。この性質は工学で利用されることがある。具体的には、直線路からある曲率のカーブに侵入するとき、いきなりカーブに接続してしまうと、曲率の変化率が大きく不快である。車の運転で言えば、急ハンドルを切らなければならない。そこで、オイラー螺旋を経由して曲率を少しずつ上げながら(ハンドルを少しずつ回しながら)カーブに接続するという方法が考えられている。このような「つなぎ」の曲線は緩和曲線(transition curve / spiral easement)と呼ばれている。

数学