標準正規分布に従う確率変数のコサインの期待値
命題
標準正規分布$N(0, 1)$に従う確率変数$X$について、$\cos{X}$の期待値は$\frac{1}{\sqrt{e}}$である。
証明1
標準正規分布の確率密度関数は、
$$ f(x) = \frac{1}{\sqrt{2 \pi}}\exp{[-\frac{x^2}{2}]} $$
であるから、$\cos{X}$の期待値は
$$ E[\cos{X}] = \int_{-\infty}^{\infty}\cos{x} \cdot f(x)dx = \int_{-\infty}^{\infty}\cos{x}\frac{1}{\sqrt{2 \pi}}\exp{[-\frac{x^2}{2}]}dx $$
なので、この積分を計算する。
$\cos{x} = \frac{e^{ix} + e^{-ix}}{2}$により次のようになる。
$$ E[\cos{X}] = \frac{1}{2\sqrt{2 \pi}} \int_{-\infty}^{\infty}\exp{[-\frac{x^2}{2} + ix]}dx + \frac{1}{2\sqrt{2 \pi}} \int_{-\infty}^{\infty}\exp{[-\frac{x^2}{2} - ix]}dx $$
$t = -x$の置換積分により、右辺の第一項と第二項は同じであることが示されるので
$$ E[\cos{X}] = \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty}\exp{[-\frac{x^2}{2} - ix]}dx $$
を計算すればよい。
被積分関数の指数の肩を平方完成すると、
$$ E[\cos{X}] = \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty}\exp{[-\frac{(x + i)^2}{2} - \frac{1}{2}]}dx = \frac{1}{\sqrt{e} \cdot \sqrt{2 \pi}} \int_{-\infty}^{\infty}\exp{[-\frac{(x + i)^2}{2}]}dx $$
$z = x + i$により置換すると、
$$ E[\cos{X}] = \frac{1}{\sqrt{e} \cdot \sqrt{2 \pi}} \int_{i -\infty}^{i + \infty}\exp{[-\frac{z^2}{2}]}dz $$
なる複素積分となる。
ここで、正の実数$R$を取り、$-R, -R + i, R + i, R$の各点を結ぶ長方形の積分路を考える。
$$ C_1 : -R \to -R+i $$
$$ C_2 : -R+i \to R+i $$
$$ C_3 : R+i \to R $$
$$ C_4 : R \to -R $$
$$ C : C_1 + C_2 + C_3 + C_4 $$
とする。
$C$は単純閉曲線であり、$\exp{[-\frac{z^2}{2}]}$は正則であるから、Cauchyの積分定理により、
$$ \int_{C}\exp{[-\frac{z^2}{2}]}dz = 0 $$
また、$R$が十分に大きいとき、
$$ \left|\int_{C_1}\exp{[-\frac{z^2}{2}]}dz\right| = \left|\int_{0}^{1}\exp{[-\frac{(-R+it)^2}{2}]}dt\right| \le \int_{0}^{1}\left|\exp{[-\frac{(-R+it)^2}{2}]}\right|dt = \int_{0}^{1}\exp{[-\Re{\frac{(-R+it)^2}{2}}]}dt = \int_{0}^{1}\exp{[-\frac{R^2 - t^2}{2}]}dt \le \int_{0}^{1}\exp{[-\frac{R^2 - 1}{2}]}dt = \exp{[-\frac{R^2 - 1}{2}]} $$
なので、$R \to \infty$の極限を取ると、
$$ \int_{C_1}\exp{[-\frac{z^2}{2}]}dz \to 0 $$
同様に、
$$ \int_{C_3}\exp{[-\frac{z^2}{2}]}dz \to 0 $$
そこで、$R \to \infty$において、
$$ \int_{C_2}\exp{[-\frac{z^2}{2}]}dz + \int_{C_4}\exp{[-\frac{z^2}{2}]}dz \to 0 $$
右辺の第二項は、実軸上でのガウス積分であり、
$$ \int_{C_4}\exp{[-\frac{z^2}{2}]}dz \to -\sqrt{2 \pi} $$
よって、
$$ \int_{C_2}\exp{[-\frac{z^2}{2}]}dz \to \sqrt{2 \pi} $$
結局、
$$ E[\cos{X}] = \frac{1}{\sqrt{e} \cdot \sqrt{2 \pi}} \int_{i -\infty}^{i + \infty}\exp{[-\frac{z^2}{2}]}dz = \frac{1}{\sqrt{e} \cdot \sqrt{2 \pi}} \lim_{R \to \infty} \int_{C_2}\exp{[-\frac{z^2}{2}]}dz = \frac{1}{\sqrt{e} \cdot \sqrt{2 \pi}} \sqrt{2 \pi} = \frac{1}{\sqrt{e}} $$
が得られる。
証明2
$\cos{x}$のマクローリン展開により、
$$ E[\cos{X}] = E[(1 - \frac{X^2}{2!} + \frac{X^4}{4!} - …)] = E[1] - \frac{E[X^2]}{2!} + \frac{E[X^4]}{4!} - … $$
そこで、
$$ I_n := E[X^{2n}] = \int_{-\infty}^{\infty} x^{2n} \frac{1}{\sqrt{2\pi}} e^{\frac{-x^2}{2}}dx $$
とおく。
部分積分により、 $$ \int_{-\infty}^{\infty} x^{2n} e^{\frac{-x^2}{2}}dx = \left[\frac{x^{2n + 1}}{2n+1} e^{\frac{-x^2}{2}}\right]_{-\infty}^{\infty} - \int_{-\infty}^{\infty} \frac{x^{2n + 1}}{2n+1} \cdot (-x) e^{\frac{-x^2}{2}}dx = 0 + \int_{-\infty}^{\infty} \frac{x^{2n + 2}}{2n+1} e^{\frac{-x^2}{2}}dx = \frac{1}{2n+1} \int_{-\infty}^{\infty} x^{2n + 2} e^{\frac{-x^2}{2}}dx $$
がわかるので、
$$ I_{n+1} = (2n + 1) I_n $$
という漸化式を得る。これを繰り返し用いて、
$$ I_n = (2n - 1)!! I_0 = (2n - 1)!! $$
となる。よって、
$$ E[\cos{X}] = I_0 - \frac{I_1}{2!} + \frac{I_2}{4!} - … = 1 - \frac{1!!}{2!} + \frac{3!!}{4!} - … = 1 - \frac{1}{2 \cdot 1} + \frac{3 \cdot 1}{4 \cdot 3 \cdot 2 \cdot 1} - … = 1 - \frac{1}{2} + \frac{1}{4 \cdot 2} - … = 1 - \frac{1}{2} \cdot \frac{1}{1!} + \frac{1}{2^2} \cdot \frac{1}{2!} - … = \sum_{n=0}^{\infty}\frac{(-\frac{1}{2})^n}{n!} = e^{-\frac{1}{2}} = \frac{1}{\sqrt{e}} $$
を得る。
補足
なお、$\sin{X}$の期待値は自明で$0$である。
これは、被積分関数が偶関数と奇関数の積になるためである。
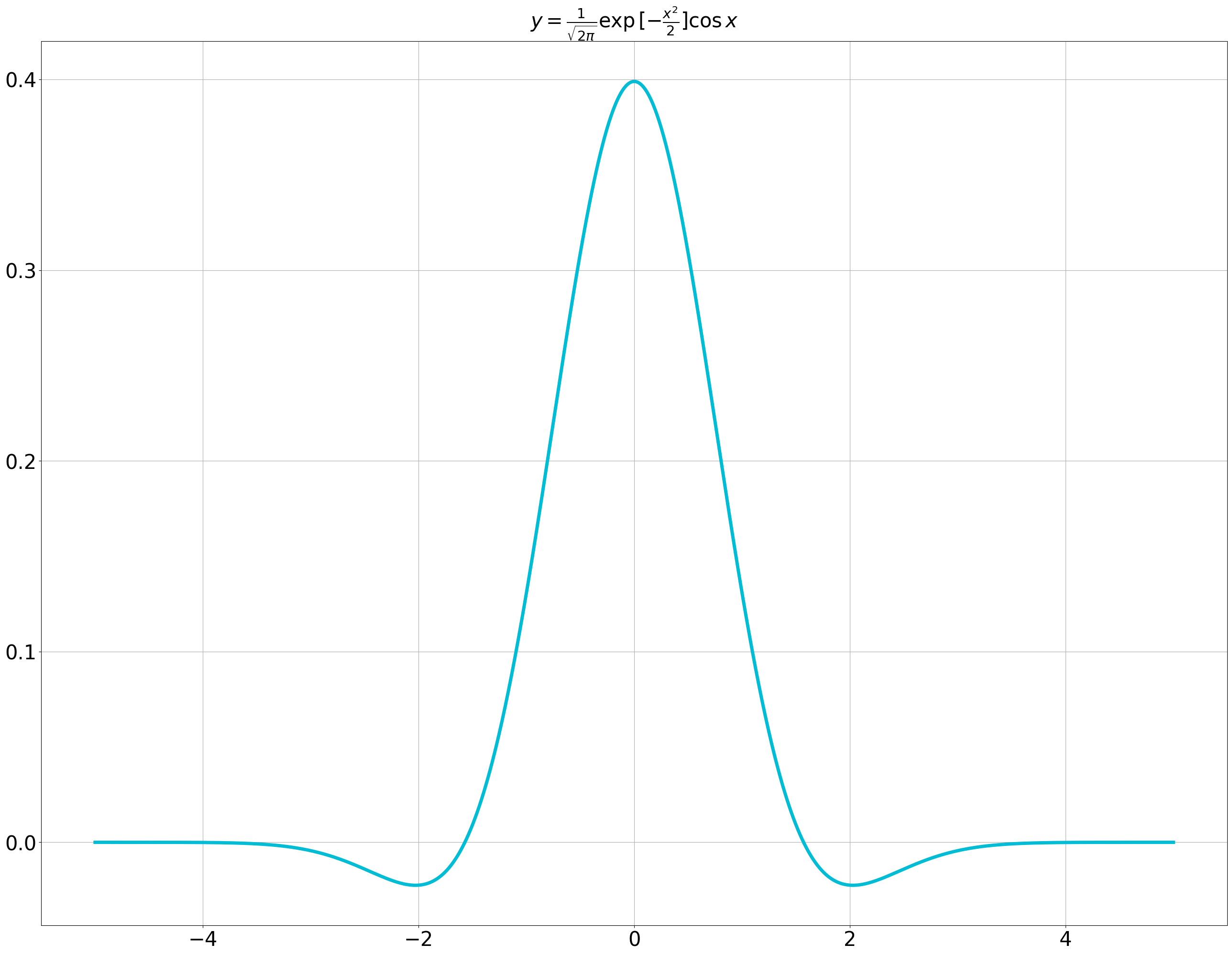
ここで検討した被積分関数のグラフは以下のようになる。ここでは、このグラフとx軸で囲まれた部分の(符号を考慮した)面積を求めたのである。
正規分布の特性関数を既知とするなら、この問題は非常に簡単である。
確率密度関数が偶関数であることから、
$$ \phi(t) = E[e^{itX}] = E[\cos(tX)] $$
であるので、特性関数
$$ \phi(t) = \exp{\left[ -\frac{t^2}{2} \right]} $$
に$t=1$を代入すれば直ちに結果が得られる。