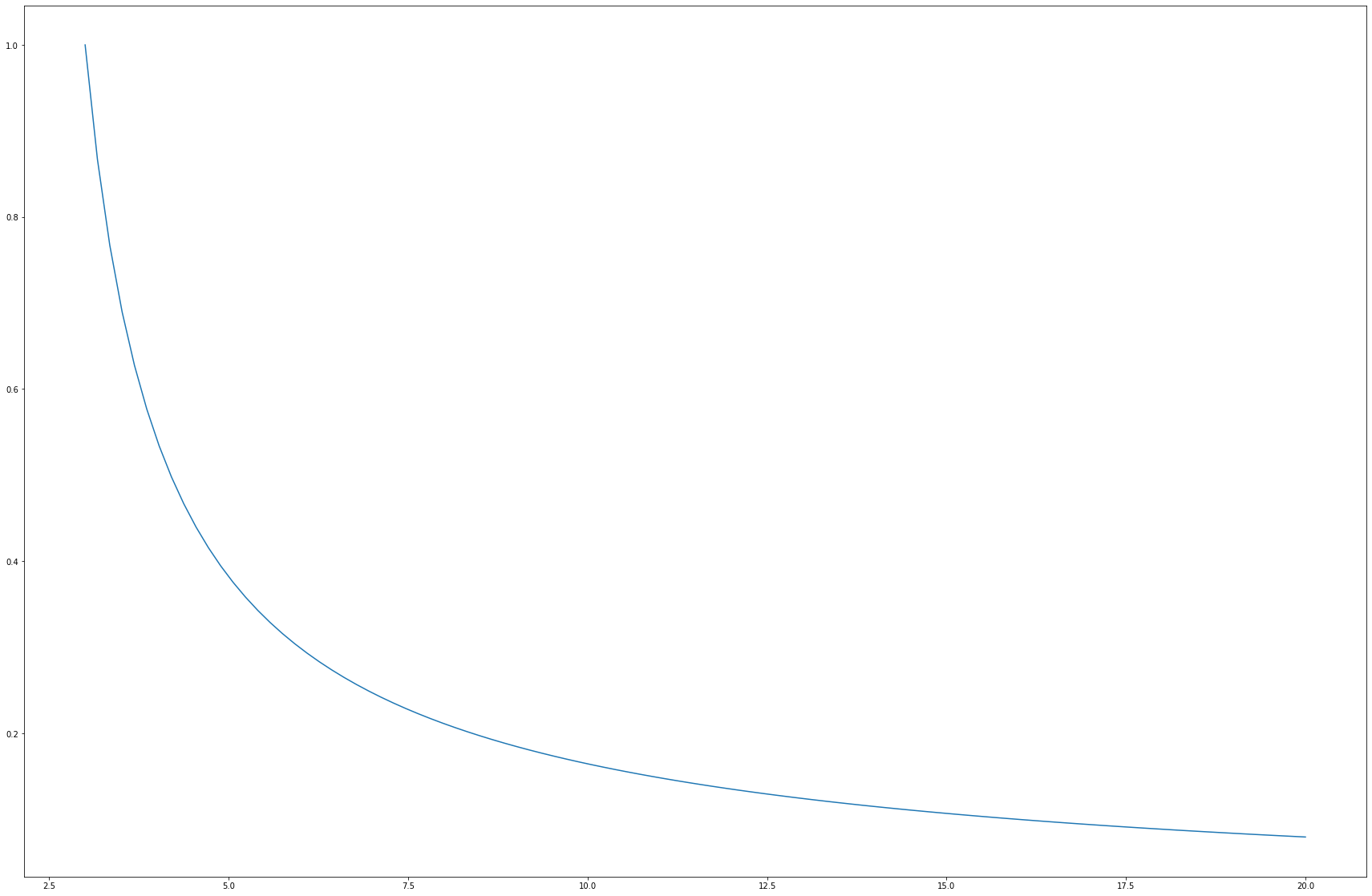
正多角形とその対角線によって作られる正多角形の相似比
命題
$n$を5以上の奇数とする。
正n角形の対角線をすべて引いたとき、内部に別の正n角形ができる。
元の正n角形と内部の正n角形の相似比$r$は、
$$
r = \frac{\sin{\frac{\theta}{2}}}{\cos{\theta}}
$$
で与えられる。
ただし、ここで、$\theta = \frac{\pi}{n}$とした。
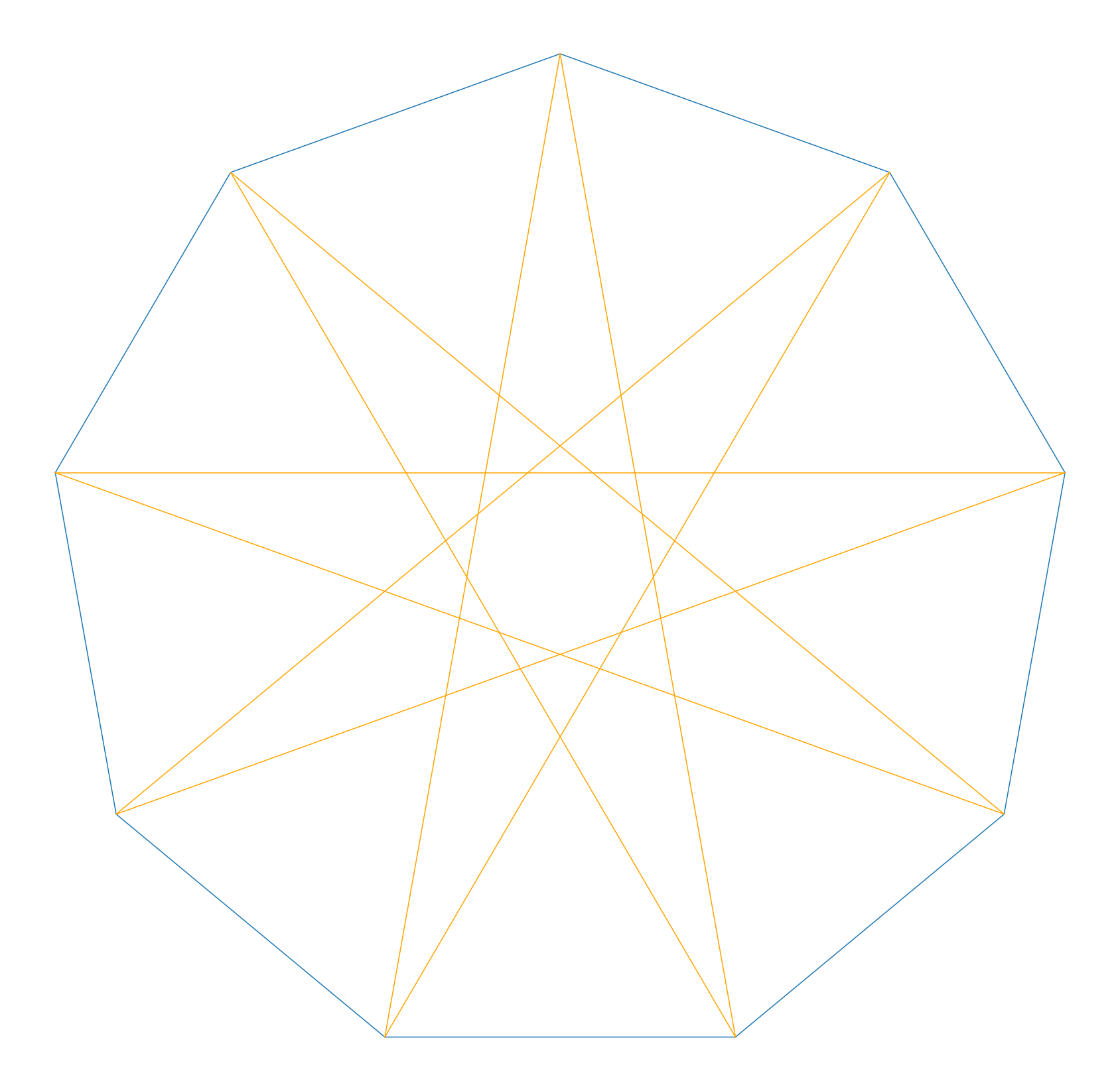
証明のスケッチ
正n角形の外接円の半径の比に注目する。
もとの外接円の半径を1として、内部にできた正n角形の外接円の半径$r$を求めれば良い。
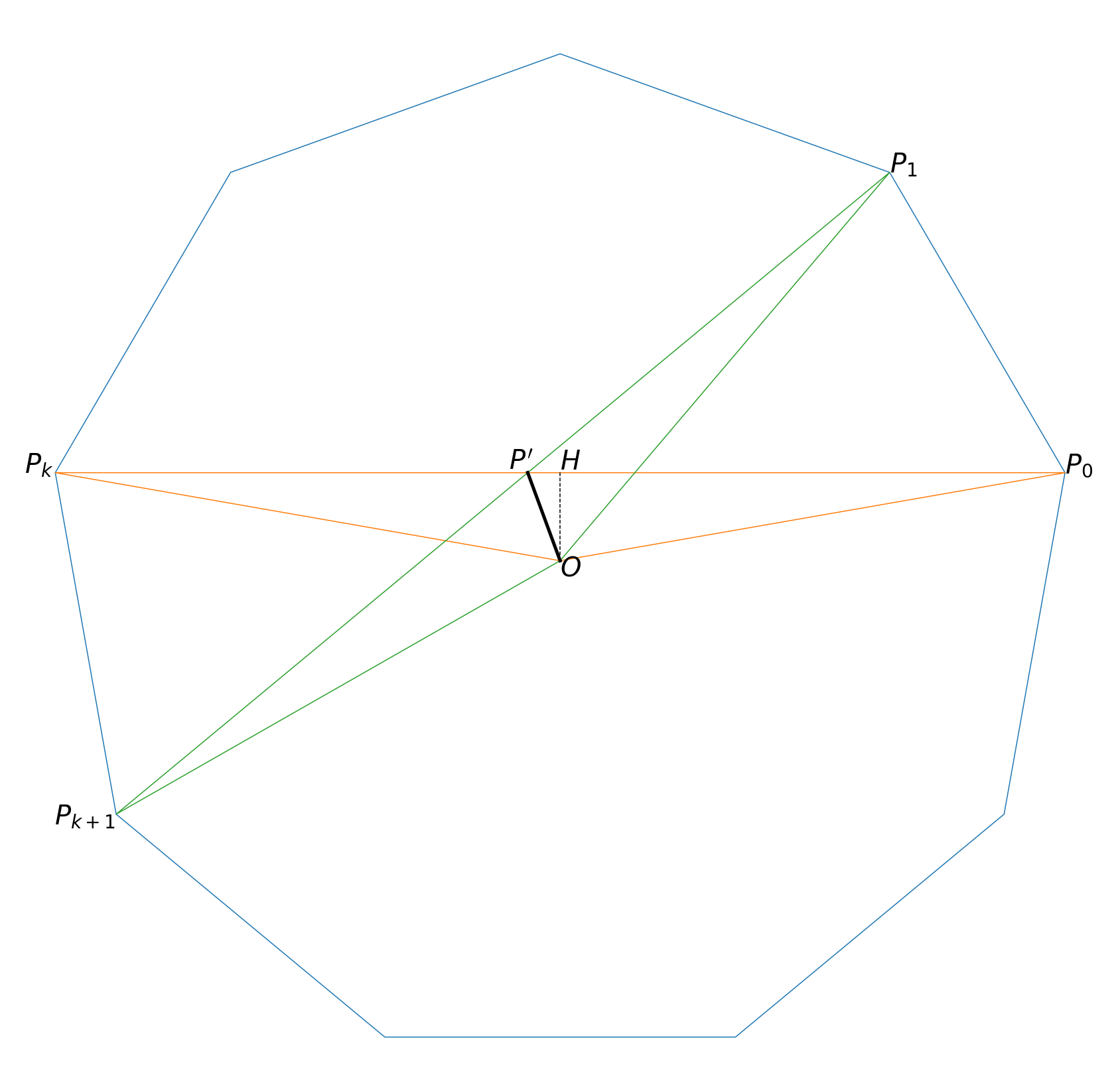
そこで、内部の正n角形の頂点を作る、2本の対角線に注目する。
$$
n = 2k + 1 \ \ (k \geq 2)
$$
とおき、元の正多角形の頂点を、
$$
P_0, P_1, …, P_k, P_{k + 1}, …, P_{2k}, P_{2k + 1}
$$
とおく。
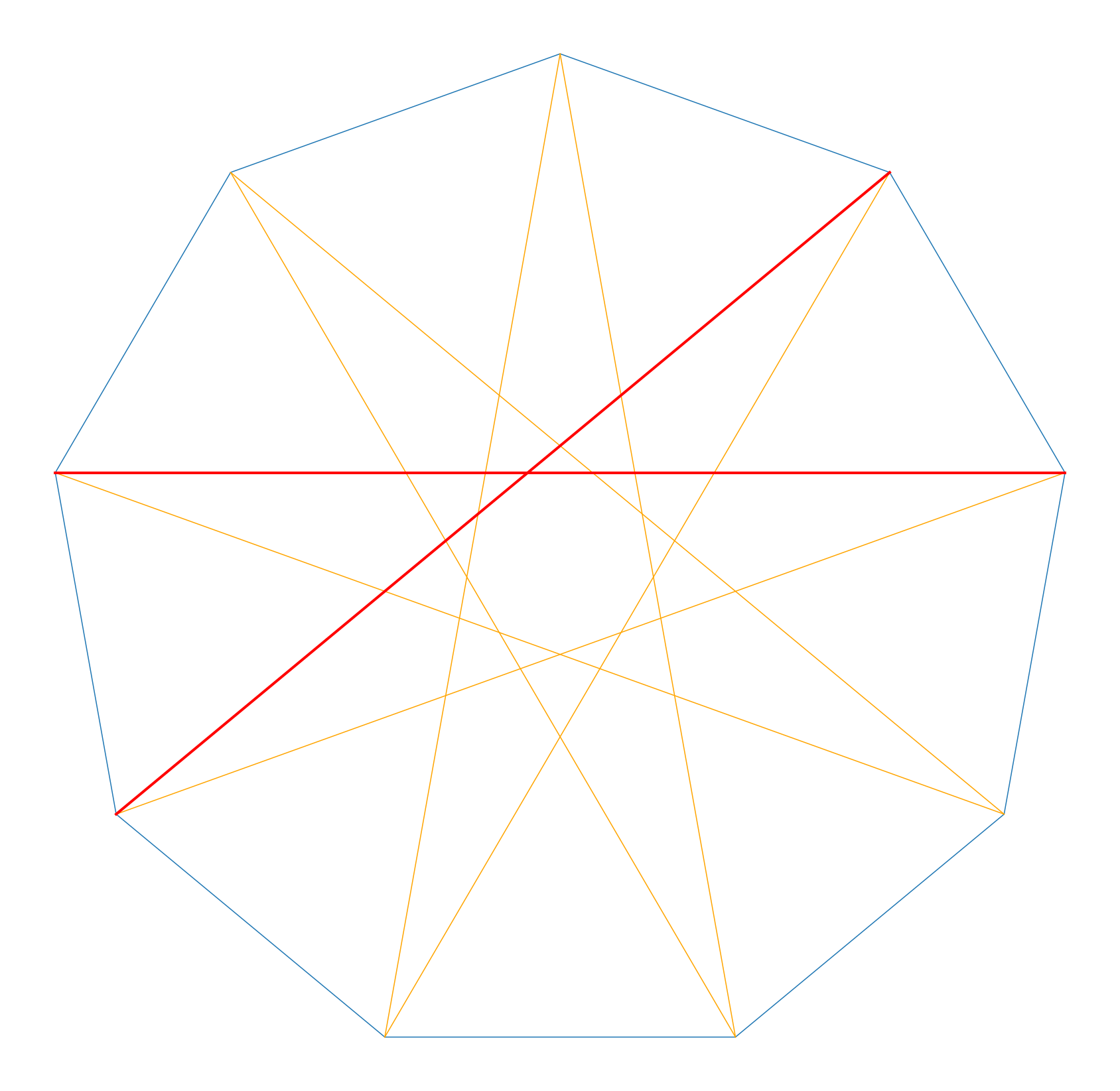
内部の正多角形の頂点を作るような対角線は、
(内部にできる正多角形の一辺となるような対角線のセットは、「中心との距離が最も短いような」対角線のセットである、という考察から、)
$$
\overline{P_0P_k},\ \overline{P_1P_{k + 1}}, …
$$
であることがわかる。
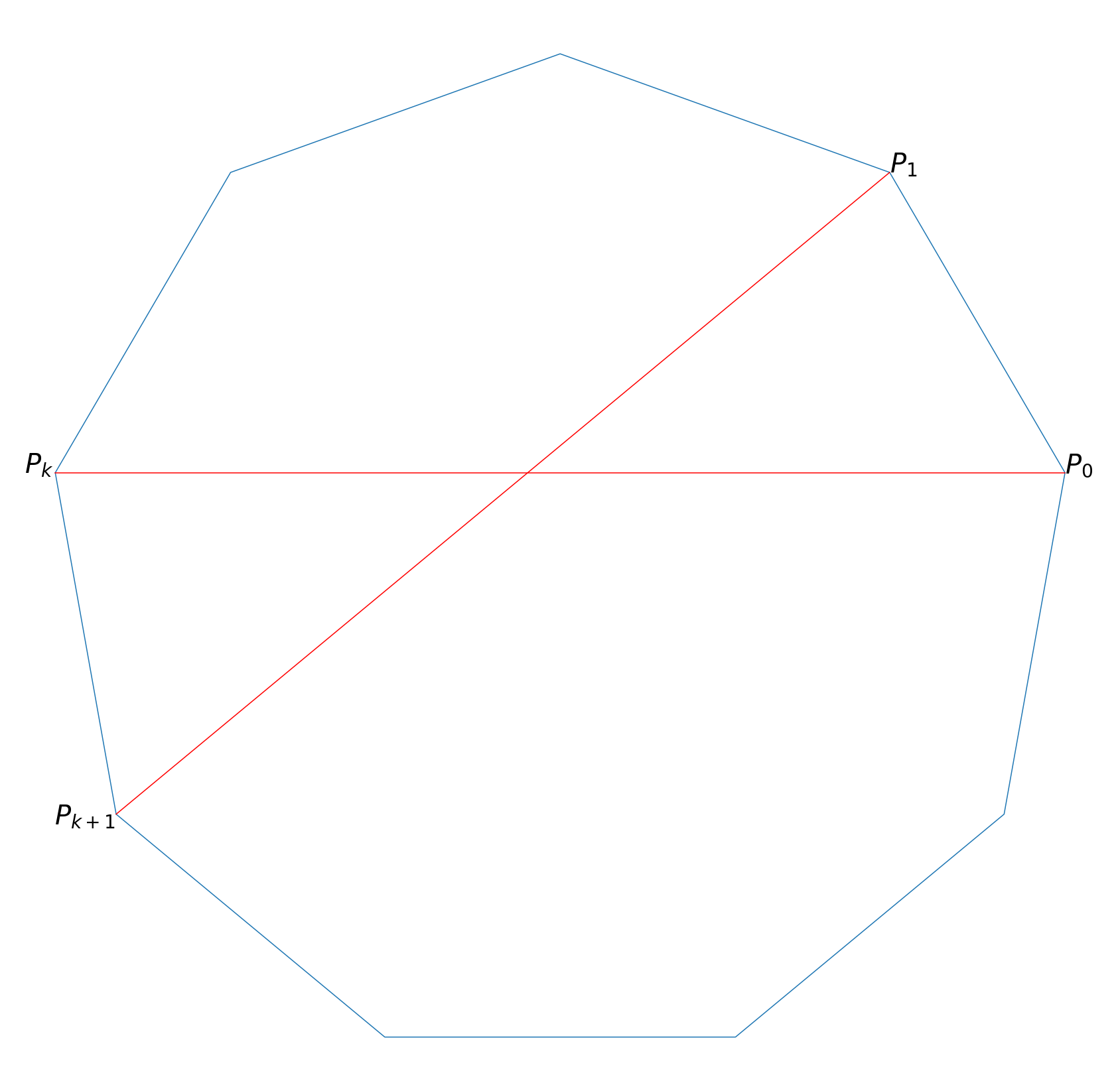
対称性から、対角線$\overline{P_0P_k}$, $\overline{P_1P_{k + 1}}$の交点$P’$について、$OP’$の長さを考えることにする。
中心$O$から、$\overline{P_0P_k}$に下ろした垂線の足を$H$とすると、
$$
\angle OP_0H = \frac{1}{2} (\pi - \angle P_0OP_k) = \frac{1}{2} (\pi - k \angle P_0OP_1)
= \frac{1}{2} (\pi - k \frac{2\pi}{2k + 1}) = \frac{\pi}{2n}= \frac{\theta}{2}
$$
であることから、
$$
OH = \sin{\frac{\theta}{2}}
$$
また、$P’H$は内部の正多角形の一辺の半分であり、したがって、 $$ \angle HOP’ = \frac{1}{2} \frac{2 \pi}{n} = \frac{\pi}{n}= \theta $$
ゆえに、 $$ r = OP’ = \frac{OH}{\cos{\theta}} = \frac{\sin{\frac{\theta}{2}}}{\cos{\theta}} $$
補足
$$ r(n) = \frac{\sin{\frac{\pi}{2n}}}{\cos{\frac{\pi}{n}}} $$ は、$(2,\infty)$上の連続関数に拡張できて、グラフは以下のようになる。
