モンティ・ホール問題のシミュレーション
モンティ・ホール問題とはなにか?
モンティ・ホール問題は直感に反する結果をもたらす確率の問題として知られている。
“Let’s Make a Deal"というアメリカのテレビ番組を下敷きにしており、問題自体の初出は以前に遡るものの、 1990年に雑誌に投稿されたことがきっかけとなり広く知られるようになった。
その投稿に書かれた問題は次のようなものであった。
あなたはゲーム番組に出演しています。
あなたは、3つのドアのうち一つを選択することになります。
1つのドアの後ろにだけ景品の車があり、他のドアの後ろにはヤギがいます(ハズレです)。
あなたが選んだドアを1番とすると、ドアの後ろに何があるのかを知っている司会者が、ヤギがいる別のドアを開きます (3番とします)。
司会者は次に、「2番のドアを選びますか?」と尋ねます。
選択を変えることはあなたにとって有利でしょうか?
答えから言うと、「選択を変えることは有利である」。
この答えは多くの人の直感に反していたため、議論を呼ぶこととなった。
この記事では、モンティ・ホール問題の答えについて詳しい解説はせず(他の多くのウェブサイトで千言万語で説明されている)、シミュレーションでこの結果を確かめてみようと思う。
シミュレーションの概要
次の3つの異なる戦略を取るプレイヤーを想定し、それぞれのプレイヤーについてゲームを10000回実行する。
10000回までの勝率の変化をグラフにする。
1. 頑固なプレイヤー (Stubborn Player)
頑固なプレイヤーは、一つのヤギのドアが開けられた後も、最初の選択を変えない。
2. 気まぐれなプレイヤー (Capricious Player)
気まぐれなプレイヤーは、一つのヤギのドアが開けられた後も、最初の選択を変えたり、変えなかったりする。
気分によってランダムにその選択をする。
3. 柔軟なプレイヤー (Flexible Player)
柔軟なプレイヤーは、一つのヤギのドアが開けられた後、必ず、最初とは異なるドアを選択し直す。
シミュレーション結果
シミュレーションの結果は以下のようになる。
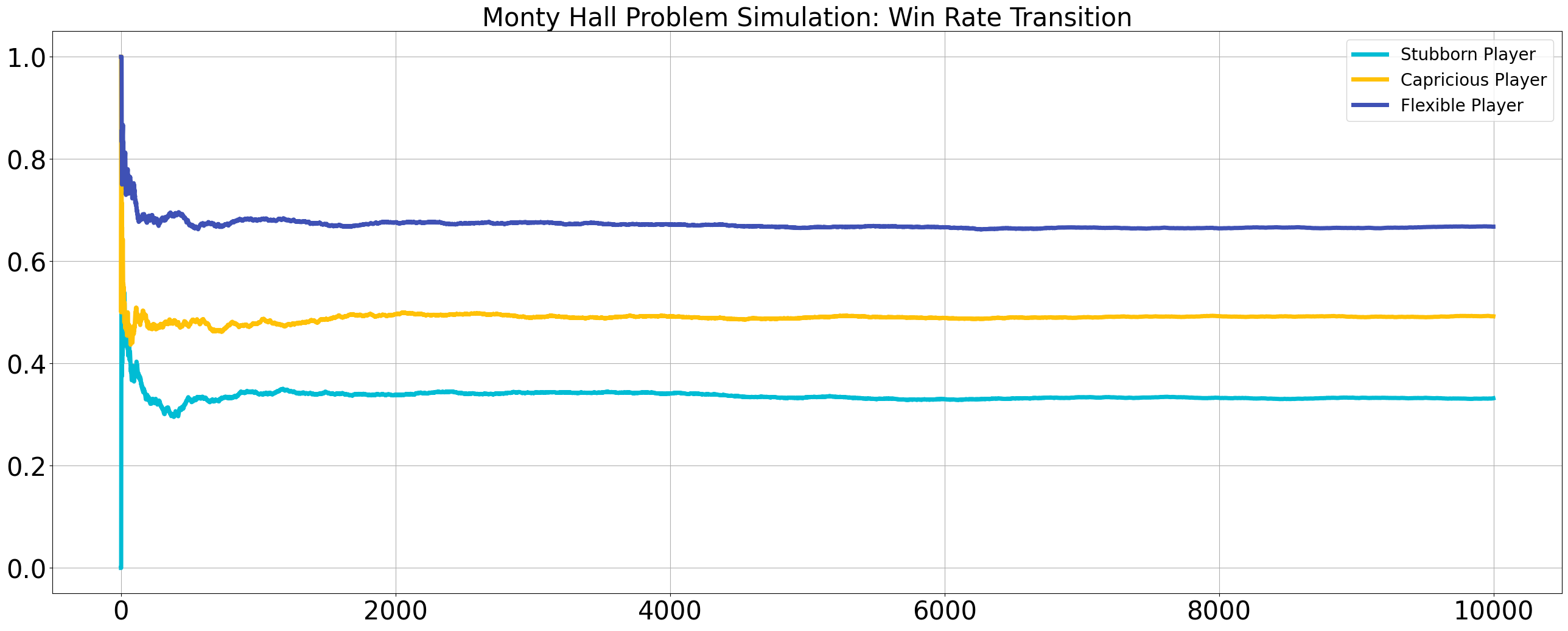
10000回の試行後の結果に着目すると、
- 頑固なプレイヤーが最も勝率が悪く、およそ
- いっぽう、柔軟なプレイヤーは最も勝率が高く、およそ
- 気まぐれなプレイヤーはその中間で、およそ
これは、計算と一致する。
シミュレーションコード
Pythonで記述したシミュレーションコードを以下に示す。
シミュレーションコードを精査することで、直感に反する結果となった原因がどこにあるかが理解されるだろう (ポイントはMontyHallのopen()メッソドである)。
#! /usr/bin/env python
import abc
from dataclasses import dataclass
from random import choice, randint
import numpy as np
from matplotlib import pyplot as plt
@dataclass
class Player(abc.ABC):
"""プレイヤーの抽象基底クラス"""
selected: None | int = None
"""前回の選択肢を保存する"""
def __init__(self):
pass
def select(self) -> int:
"""最初の選択"""
self.selected = randint(1, 3)
return self.selected
@abc.abstractmethod
def reselect(self, opened: int) -> int:
"""ハズレを一つ教えてもらったあとの再選択
具象クラスで実装する
"""
pass
class StubbornPlayer(Player):
"""ハズレを一つ教えてもらった後、最初と選択を変えない戦略を取る頑固なプレイヤー"""
def reselect(self, opened: int) -> int:
if self.selected is None:
raise ValueError("Not selected yet")
return self.selected
class CapriciousPlayer(Player):
"""ハズレを一つ教えてもらった後、ランダムに選択を変えたり変えなかったりする気まぐれなプレイヤー"""
def reselect(self, opened: int) -> int:
if self.selected is None:
raise ValueError("Not selected yet")
s = {1, 2, 3} - {opened}
return choice(list(s))
class FlexiblePlayer(Player):
"""ハズレを一つ教えてもらった後、最初と異なるものを選択し直す戦略を取る柔軟なプレイヤー"""
def reselect(self, opened: int) -> int:
if self.selected is None:
raise ValueError("Not selected yet")
s = {1, 2, 3} - {self.selected, opened}
assert len(s) == 1
return s.pop()
@dataclass
class MontyHall:
"""ゲームマスター: モンティ・ホール"""
answer: int
"""モンティホールは答えを知っている"""
def __init__(self) -> None:
self.answer = randint(1, 3)
def open(self, selected: int) -> int:
"""選んだもの以外のハズレを1つ教える"""
s = {1, 2, 3} - {self.answer, selected}
return choice(list(s))
def check_the_answer(self, selected: int) -> bool:
"""解答をチェック
return: True: 正解, False: 不正解
"""
return selected == self.answer
def game(player: Player, monty_hall: MontyHall):
"""ゲームを実施"""
selected = player.select()
opened = monty_hall.open(selected)
selected = player.reselect(opened)
if monty_hall.check_the_answer(selected):
print("Win!")
return True
else:
print("Lose...")
return False
def win_rates(results: list[bool]) -> np.ndarray:
"""勝率の推移を計算"""
r = np.asarray(results)
return np.cumsum(r) / np.arange(1, len(r) + 1)
def main():
stu_results = []
for _ in range(10000):
result = game(StubbornPlayer(), MontyHall())
stu_results.append(result)
cap_results = []
for _ in range(10000):
result = game(CapriciousPlayer(), MontyHall())
cap_results.append(result)
flex_results = []
for _ in range(10000):
result = game(FlexiblePlayer(), MontyHall())
flex_results.append(result)
plt.rcParams["figure.figsize"] = (32.0, 12.0)
plt.plot(win_rates(stu_results), label="Stubborn Player", color="#00BCD4", lw=5)
plt.plot(win_rates(cap_results), label="Capricious Player", color="#FFC107", lw=5)
plt.plot(win_rates(flex_results), label="Flexible Player", color="#3F51B5", lw=5)
plt.title("Monty Hall Problem Simulation: Win Rate Transition", fontsize=30)
plt.legend(fontsize=20)
plt.xticks(fontsize=30)
plt.yticks(fontsize=30)
plt.grid()
plt.savefig("monty_hall_sim.png", bbox_inches="tight", transparent=True)
if __name__ == "__main__":
main()