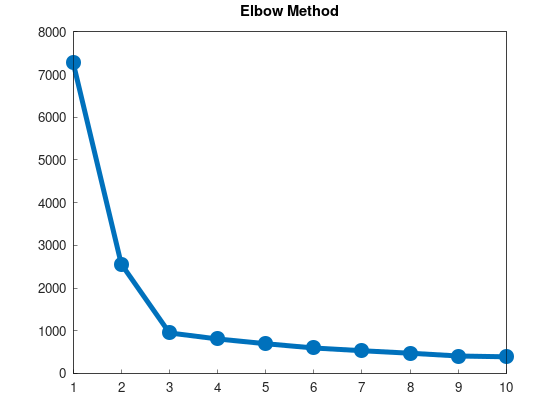
k-meansのエルボー法

January 11, 2025

性能評価指標SSE

前回、k-means++を実装して、プレーンなk-meansと比較した際に、

左上の243番目の点と左下の21番目の点が別のクラスターに分類されている => 成功
左上の243番目の点と左下の21番目の点が同じクラスターに分類されている => 失敗

というヒューリスティックなやり方で成功/失敗を判定したが、もっと良いやり方がある。

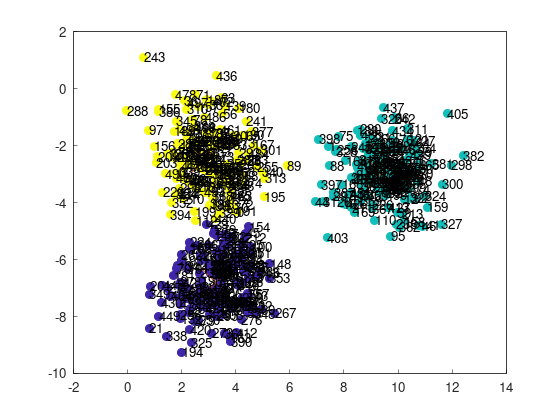
各k平均法の結果に対して、SSE(Sum of Squared Error)と呼ばれる指標を計算して、その大小によって、「推定の良さ」を測るのである。

SSEは、各データ点について割り当てられたクラスター重心との距離の2乗を計算し、その和を取ったものである。

もしクラスタリングがうまくいっていれば、割り当てられたクラスター重心との距離は小さくなるので、SSEは小さくなり、うまくいっていなければ、SSEは大きくなるだろう、というわけである。

そもそもk-meansは、ラベルの更新とセントロイドの更新によって、SSEの最小化(最適化)を図るアルゴリズムであるというふうに捉えられるので、SSEを指標として用いるのは自然でもある。

前回実装したKMeansクラスにsseフィールドを追加し、update_labels()関数の中で更新するようにしておこう。

sse = 0;
for (int i = 0; i < m; ++i)
{
    double min_dist = std::numeric_limits<double>::max();
    int min_label = -1;
    for (int j = 0; j < k; ++j)
    {
        double dist = distance(points[i], centroids[j]);
        if (dist < min_dist)
        {
            min_dist = dist;
            min_label = j;
        }
    }
    if (labels[i] != min_label)
    {
        updated = true;
        labels[i] = min_label;
    }
    sse += min_dist * min_dist;
}

このSSEはscikit-learnのKMeansクラスでは、inetia_フィールドとしてアクセス可能である。

公式では以下のように説明している。

inertia_: float
Sum of squared distances of samples to their closest cluster center, weighted by the sample weights if provided.

k-meansを何度か試行して、最も良い結果を選ぶ

前回、k-means++をあるデータセットに対して適用した結果、成功率は82.2%から92.7%に上昇した。

しかし、逆に言えば、7.3%の確率で失敗してしまうわけであり、これは状況によっては実用的ではないだろう。

そこで、初期値の選び方を変えながら複数回k-means++を行って、最もSSEの結果が良かった(小さかった)結果を選択するようにすれば、成功率をより上げることができる。

1回での成功率を$p$とすれば、$n$回試行することによる成功率$p_n$は、$n$回連続失敗する確率の排反として、

$$ p_n = 1 - (1 - p)^n $$

と求まる。

$p = 0.927$であれば、

$$ p_2 = 0.994671 $$

$$ p_3 = 0.999610983 $$

$$ p_4 = 0.999971601759 $$

$$ p_5 = 0.999997926928407 $$

であるから、劇的に改善される。

これを行う関数を追加しておこう。

// k-means++をn回実行し、SSEが最良のものを返す
template <KMeansablePoint Point>
std::unique_ptr<KMeans<Point>> kmeans_plus_plus_multi(int n, int k, int max_iter, const std::vector<Point> &points)
{
    // 最良のk-means法の結果を格納する変数
    auto kmeans_opt = std::make_unique<KMeans<Point>>(k, max_iter, points);
    kmeans_opt->sse = std::numeric_limits<double>::max();

    // k-means法を実行する変数
    auto kmeans_exc = std::make_unique<KMeans<Point>>(k, max_iter, points);

    for (int i = 0; i < n; ++i)
    {
        kmeans_exc->exec_kmeans_plus_plus();
        if (kmeans_exc->sse < kmeans_opt->sse)
        {
            kmeans_opt.swap(kmeans_exc);
        }
    }

    return kmeans_opt;
}

この実装では、std::unique_ptr::swapを使用して、コピーをできるだけ避けるように工夫した。

クラスタ数を決定するのにSSEを利用する

クラスタ数kを事前に与えなければならないのが、k平均法の面倒な点なのであるが、この性能指標SSEはクラスタ数を決定するのにも使える。

kを変えながらk平均法を実行してSSEの変化をプロットして、SSEの減少が打ち止めになるところを探すのである。

「データ点数 ≦ クラスタ数」のとき、データはすべて独立のクラスタに分類され、そのときSSEは0になる。

クラスタ数に対してSSEは単調減少になることが期待されるのであるが、どこかでその減少度合いが打ち止めになるところがあり、そこを最適なクラスタ数と考えれば良い。

数値的に具体的な方法を教えてくれるわけではないが、この手法は有名でエルボー法(Elbow method)と呼ばれている。

打ち止めになるところが肘のように見えることからこの名がついている。

example/example_kmeans_elbow_blobs_2d.cppに、このk vs SSEをプロットする実装を行った。

int main()
{
	std::vector<double> sses(10);
	std::vector<double> ks(10);
	for (int k = 1; k <= 10; ++k)
	{
		auto kmeans = yhok::cluster::kmeans_plus_plus_multi(5, k, 100, dataset_blobs_2d);
		sses[k - 1] = kmeans->sse;
		ks[k - 1] = k;
	}
	matplot::plot(sses);
	matplot::title("Elbow Method");
	matplot::show();

	return 0;
}

結果は以下の通りである。実際に「ひじ」のようなものが見えているのが確認できる。

この場合、k = 3が、それらしいクラスタ数であると判断できよう。