k-means++
k-means++とは
前回、k-meansを実装してみたが、その改良版がk-means++である。
プレーンなk-meansと比較すると、セントロイドの初期位置の選び方だけが異なるのだが、多くの場合より早く、より良い結果に収束するのだという。
2007年に発表された次の論文で示された手法である。
Arthur, D. and Vassilvitskii, S. (2007). “k-means++: the advantages of careful seeding”. Proceedings of the eighteenth annual ACM-SIAM symposium on Discrete algorithms. Society for Industrial and Applied Mathematics Philadelphia, PA, USA. pp. 1027–1035.
ここなどで読むことができる。
https://theory.stanford.edu/~sergei/papers/kMeansPP-soda.pdf
これを実装して、プレーンなk-meansと実行結果を比較してみたので、その内容について説明する。
リポジトリは前回と同じ
https://github.com/hokacci/cluster/tree/main
である。
k-meansでのセントロイドの初期化方法
もとのプレーンなk-meansの初期化はKMeans::init_centroids()関数で行っている。
内容は以下の通りである。
// セントロイドを初期化
// pointsからランダムにk個の点を選ぶ
void init_centroids()
{
std::random_device seed_gen;
std::mt19937 engine(seed_gen());
std::uniform_int_distribution<> distribution(0, m - 1);
std::vector<int> used_indices;
for (auto &¢roid : centroids)
{
// 重複しないようにindexを選ぶ
int index;
do
{
index = distribution(engine);
} while (std::find(used_indices.begin(), used_indices.end(), index) != used_indices.end());
centroid = points[index];
used_indices.push_back(index);
}
}
重複しないようにしている以外は特に難しい点はなく、与えられたデータ点の中から一様ランダムにk個を選んでセントロイドとして設定しているだけである。
k-means++でのセントロイドの初期化方法
このプレーンなk-meansの初期化方法では、偶然にも選んだセントロイドがどこかに密集していると失敗しやすく、また、イテレーションの回数も増えると考えられる。
そこで、k-means++では、最初のセントロイドができるだけ密集しないように工夫する。
具体的には、すでに選んだセントロイドの中で最も近いものとの距離の2乗に比例するようにデータ点に離散確率分布を設定し、その分布に従って次のセントロイドを選ぶ、ということをする。
具体的な実装は以下の通りである。
void init_centroids_kmeans_plus_plus()
{
std::random_device seed_gen;
std::mt19937 engine(seed_gen());
std::uniform_int_distribution<> uniform_distribution(0, m - 1);
// 最初のセントロイドはランダムに選ぶ
int index = uniform_distribution(engine);
centroids[0] = points[index];
// 残りのセントロイドは、それまでのセントロイドとの距離が遠い点が選ばれやすいような確率分布を使って選ぶ
// この場合、重複を考慮する必要はない (すでに選ばれたセントロイドは選ばれる確率が0となるため)
for (int i = 1; i < k; ++i)
{
std::vector<double> dist2s(m);
for (int j = 0; j < m; ++j)
{
double min_dist = std::numeric_limits<double>::max();
for (int l = 0; l < i; ++l)
{
min_dist = std::min(min_dist, distance(points[j], centroids[l]));
}
dist2s[j] = min_dist * min_dist;
}
std::discrete_distribution<> distance_based_distribution(dist2s.begin(), dist2s.end());
index = distance_based_distribution(engine);
centroids[i] = points[index];
}
}
まず、最初のセントロイドは一様ランダムに選ぶのだが、それ以降は距離の2乗に応じた確率分布で選んでいる。
C++の標準ライブラリにあるstd::discrete_distributionはこのようなことをしてくれる便利なクラスである。正規化も勝手にしてくれる。
なお、k-meansでは重複しないような配慮をしていたが、この方法だと、すでにセントロイドとして選ばれたデータ点には確率0が設定されるので、重複について配慮する必要もない。
性能改善の確認準備
実際に、k-means++にすることによって性能が改善するかを調べてみる。
プレーンなk-meansを実行するexec()関数に追加して、k-means++を実行するexec_kmeans_plus_plus()関数を用意しておき、イテレーション数を返すようにしておく。
これでイテレーション数の観点で比較ができるようになる。
// k-means++を実行する
// 返り値はイテレーション回数
int exec_kmeans_plus_plus()
{
init_centroids_kmeans_plus_plus();
update_labels();
int i = 0;
for (; i < max_iter; ++i)
{
update_centroids();
bool updated = update_labels();
if (!updated)
{
break;
}
}
return i;
}
次に、うまくいくか失敗するかの観点での性能評価方法を考える。
前回のk-meansでは、だいたい感覚値としては5回に1回くらいの割合で、次のように失敗することがわかった。
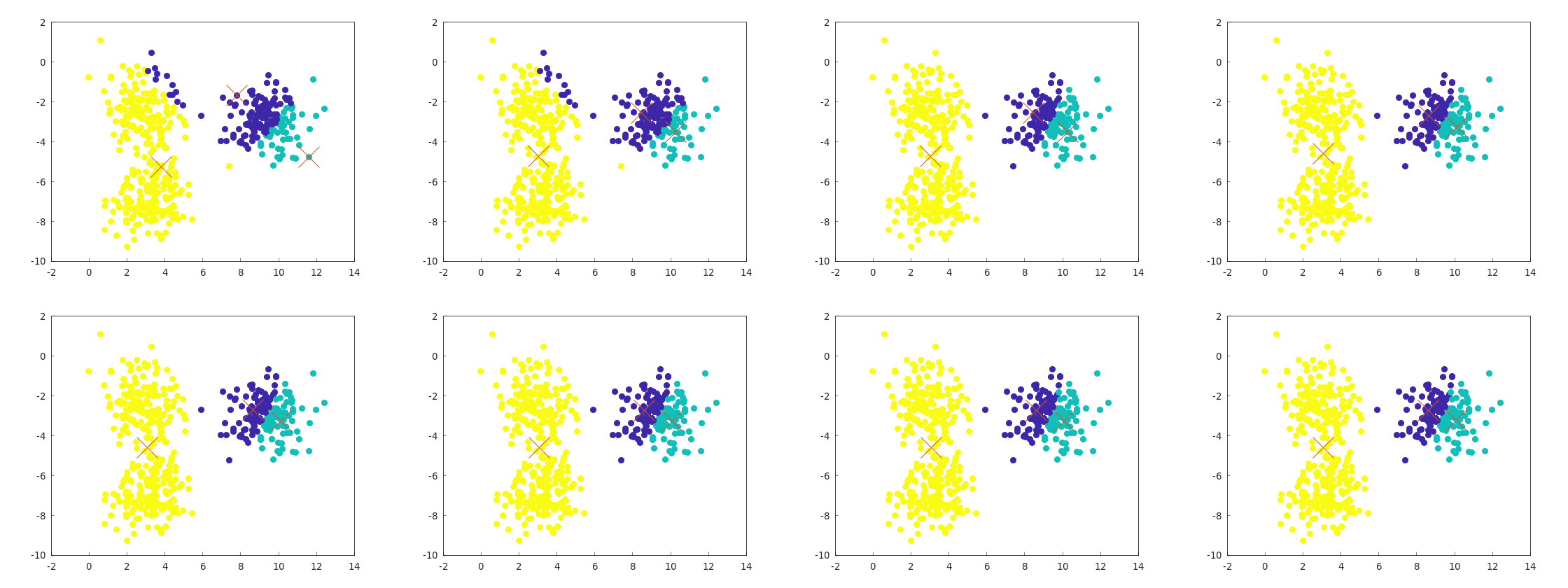
逆にこれ以外の失敗例は、何回か実行する中では発生しなかったので、この手の失敗がどれくらい起きるかという観点で性能評価をすることにする。
各点のインデックスを表示すると、次のようになる。
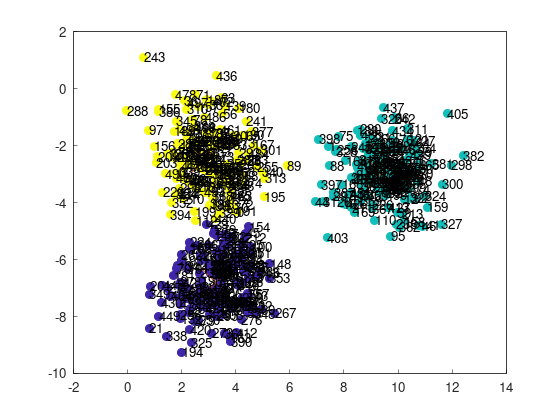
これと典型的な失敗例・成功例を見比べて、
- 左上の243番目の点と左下の21番目の点が別のクラスターに分類されている => 成功
- 左上の243番目の点と左下の21番目の点が同じクラスターに分類されている => 失敗
として、どれくらいの割合で失敗が発生するかを測定してみる。
性能改善の評価
example/example_kmeans_plus_plus_blobs_2d.cppに性能比較のコードがある。
10万回、プレーンなk-meansとk-means++を実行して、失敗率とイテレーション数の平均を計測し、表示するプログラムである。
int main()
{
yhok::cluster::KMeans kmeans(3, 100, dataset_blobs_2d);
int n = 100000;
// k-meansをn回実行して、失敗する回数を数える
int count_failure = 0;
int sum_iterations = 0;
for (int i = 0; i < n; ++i)
{
int iterations = kmeans.exec();
sum_iterations += iterations;
if (kmeans.labels[243] == kmeans.labels[21])
{
++count_failure;
}
}
std::cout << "Failure rate (k-means): " << count_failure / static_cast<double>(n) << std::endl;
std::cout << "Average number of iterations: " << sum_iterations / static_cast<double>(n) << std::endl;
// k-means++をn回実行して、失敗する回数を数える
count_failure = 0;
sum_iterations = 0;
for (int i = 0; i < n; ++i)
{
int iterations = kmeans.exec_kmeans_plus_plus();
sum_iterations += iterations;
if (kmeans.labels[243] == kmeans.labels[21])
{
++count_failure;
}
}
std::cout << "Failure rate (k-means++): " << count_failure / static_cast<double>(n) << std::endl;
std::cout << "Average number of iterations: " << sum_iterations / static_cast<double>(n) << std::endl;
return 0;
}
結果は次のようになった。
Failure rate (k-means): 0.1784
Average number of iterations: 3.92808
Failure rate (k-means++): 0.07242
Average number of iterations: 2.65308
失敗率は17.8%から7.24%に下がり(成功率は82.2%から92.7%に上がり)、イテレーション数の平均は3.92回から2.65回に下がっており、いずれの観点でも性能が向上したことが確認できる。
もちろんデータセットの性質によって結果は変わると考えられるが、k-means++の力はかくのごとし、といったところである。