k平均法をC++で実装した
k平均法とは
k平均法(k-means)は、おそらく最もよく知られたクラスタリング(clustering)アルゴリズムである。
多数の点の入力があり、これをk個のクラスターに分別する。
kという数値は指定しなければならない。
この分別は、点同士の距離(近さ)を測ることによって行われる。
機械学習には分類(classification)という言葉もあり、紛らわしいのだが、 こちらはあらかじめラベルのついた点を多数学習することにより、ラベルの付いていない新しいデータのラベルを予測することに当たる。
classificationは教師あり学習、clusteringは教師なし学習である。
k平均法は、クラスタ数をあらかじめ指定しなければならないという大きな問題がありつつも、実装のシンプルさもあり、いくつかの場面では有効である。
リポジトリ
今回、以下のリポジトリにk平均法のC++実装コードを格納した。
https://github.com/hokacci/cluster/tree/main
k平均法の動きがわかるように、シンプルな実装にしたのであって、実用上は都合の悪い点は残っている。
今回はこのリポジトリに実装したコードについて説明を行いたい。
リポジトリの構造
おおむね、次のような構造になっている。
include/kmeans.hにテンプレート化されたk平均法の実装があり、example/example_kmeans_blobs_2d.cppはそれを利用したサンプルコードである。
.
├── example
│ ├── example_kmeans_blobs_2d.cpp
│ └── helpers
│ ├── include
│ │ ├── blobs_2d.h
│ │ └── point_2d.h
│ └── src
│ ├── blobs_2d.cpp
│ └── point_2d.cpp
└── include
└── kmeans.h
k平均法のコンセプト
C++20で導入されたconceptを使用して、k平均法を行うに当たり必要となるデータの属する空間に対する制約を定義しておく。
以下が実装である。
// K-meansを実行できる点の概念
template <typename Point>
concept KMeansablePoint = requires(Point a, Point b, std::vector<Point> points) {
// 2点間の距離を計算する関数が定義されていること
{ distance(a, b) } -> std::convertible_to<double>;
// 重心を計算する関数が定義されていること
{ center(points) } -> std::convertible_to<Point>;
};
k平均法では、「2点間の距離を測る」・「複数の点の重心を計算する」という2つの操作が必要である。
もちろん通常のユークリッド空間では、これら2つの操作は自然に行うことができるのだが、このようにコンセプトを定義することで、k平均法の重要なポイントが顕になる。
名前にあるように平均、すなわち重心を計算することが肝だ、ということである (単に距離が定義されているだけではだめ)。
k平均法の大まかなフロー
続いて、k平均法の実装である。
先に定義したコンセプトを使用してテンプレートパラメーターPointを制限しておく。
k平均法の流れはexec()メンバ関数に書かれているとおりである。
template <KMeansablePoint Point>
struct KMeans
{
...
// K-means法を実行する
void exec()
{
init_centroids();
update_labels();
for (int i = 0; i < max_iter; ++i)
{
update_centroids();
bool updated = update_labels();
if (!updated)
{
break;
}
}
}
...
};
まず、init_centroids()で、k個のセントロイド(重心)をランダムに選ぶ。
つづいて、update_labels()で、各点に対して、最も近いセントロイドのインデックスでラベル付けを行う。
今度は、update_centroids()で、同じラベルの点の重心を求めることで、セントロイドを更新する。
以下、ラベルの更新が全くされないか、max_iter回ループするかするまで、ラベルの更新とセントロイドの更新を繰り返す。
非常にシンプルである。
それぞれの処理の実装は詳細を見るほどでもないのだが、update_labels()でコンセンプトにあるdistance()関数を呼び出し、
update_centroids()でコンセプトにあるcenter()関数を呼び出していることに注意しておく。
exampleの実装 (2次元データ)
つづいて、2次元データでこのk平均法を実行する例をexample/example_kmeans_blobs_2d.cppに実装してあるので、それについて説明する。
まず、最初に定義したコンセプトを満たすような構造体を定義するのであるが、それは、point_2d.(h|cpp)で行っている。
// 2次元の点を表す構造体
struct Point2D
{
double x = 0;
double y = 0;
};
// 2点間の距離を計算する
double distance(const Point2D &a, const Point2D &b)
{
return std::sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
// 重心を計算する
Point2D center(const std::vector<Point2D> &points)
{
Point2D c;
for (auto p : points)
{
c.x += p.x;
c.y += p.y;
}
c.x /= points.size();
c.y /= points.size();
return c;
}
distance()はピタゴラスの定理により測った距離であり、center()は単にベクトルの平均として実装している。特に問題はないかと思う。
このPoint2Dのサンプルのデータセットが、blobs_2d.(h|cpp)で定義されているstd::vector<Point2D> dataset_blobs_2dである。
このデータセットは、Pythonのscikit-learnでサンプルとして使われているtoy datasetである。
exampleの実装 (可視化)
example/example_kmeans_blobs_2d.cppでは、k平均法の挙動がわかるようにステップごとに可視化を行っている。
ここでは、Pythonのmatplotlibのような書き心地で使用できるmatplot++というライブラリを使用した。
各点に貼られたラベルを色で表示し、セントロイドをバツ印で表現している。
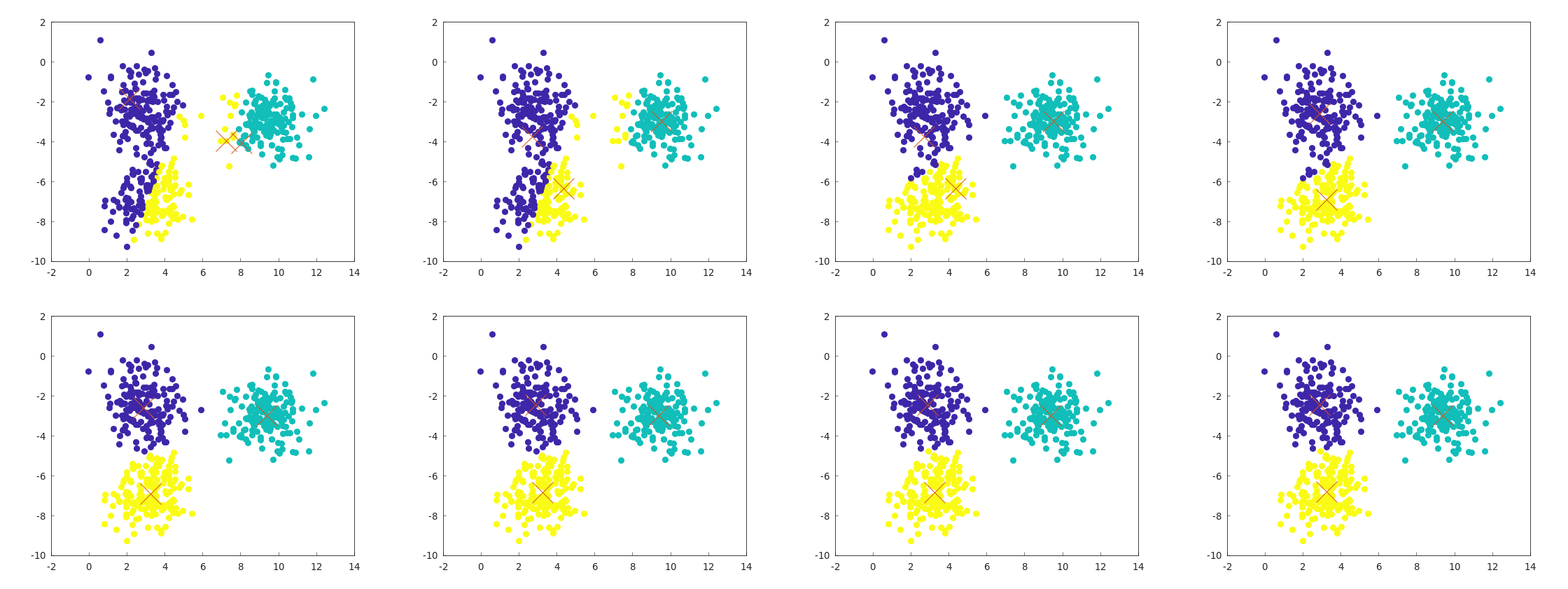
k平均法の挙動例
以下にexample_kmeans_blobs_2d.cppの実行例を示す。
左上から始まって、右下で終わる一連の流れがこれで見ることができる。
セントロイドの更新とラベルの更新が交互に発生していることも確認できる。
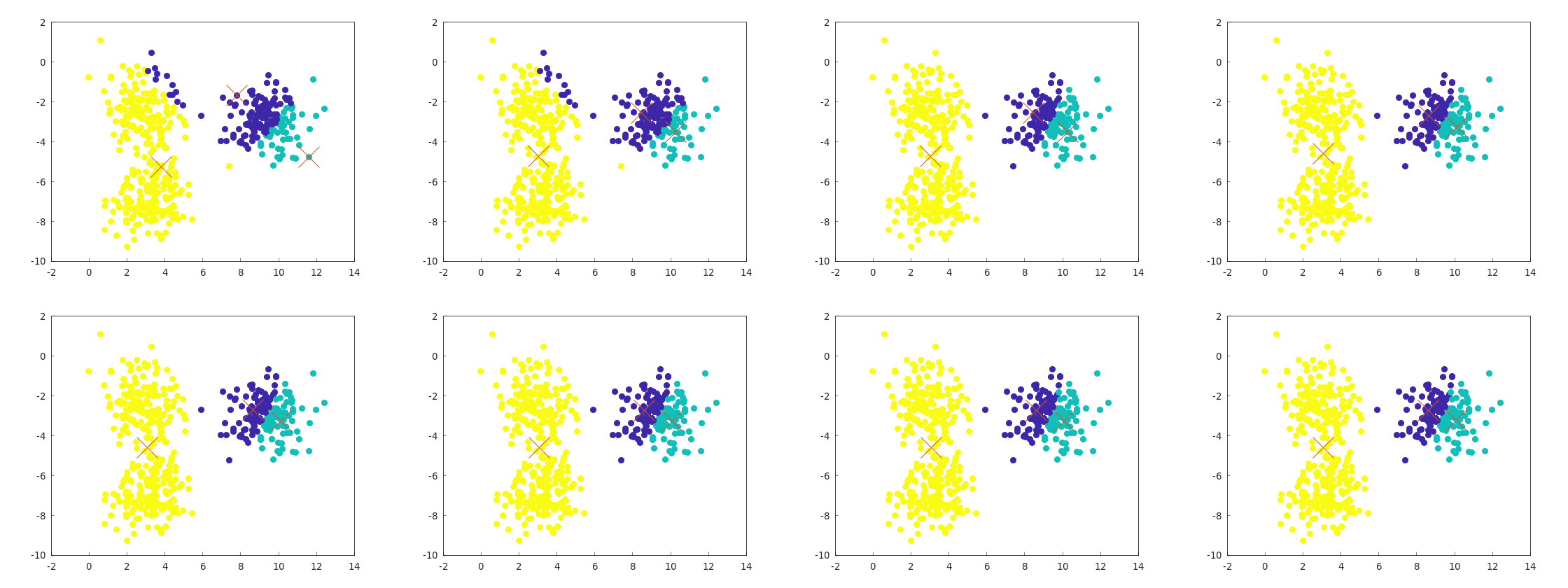
k平均法の失敗例
k平均法の悪い点として、局所解にハマることがある。以下はその例である。
ランダムに選んだ最初のセントロイドの位置が悪いと、このようになってしまう。
k-means++
k平均法の改良版としてk-means++というものもある。これは初期値の選び方を工夫したものである。
k-means++や他のクラスタリングアルゴリズムについても、気が向いたら実装してみようと思う。