FFTの使い方 (NumPy, SciPy)

2024年08月27日 (最終更新: 2025年12月06日)

翻訳: EN

FFTとはなにか?

信号処理における基本的な道具の一つに、FFTというものがある。

FFTとは、高速フーリエ変換(fast Fourier transform)の略語であり、離散フーリエ変換(DFT, discrete Fourier transform)を高速に計算するアルゴリズムである。

FFTを使ってみる

FFTのアルゴリズムは、対称性を用いて非常に早く計算できるようになっており、それ自体興味深いものであるが、ここでは原理の説明をせず、使い方の説明をしてみたい。

フーリエ変換はよく、「時間領域から周波数領域への変換である」、などと言われる。

実際どういう風になるのかを見てみよう。

今回FFTの対象とするのは音声信号である。音声信号は耳で聞けるので感覚的にも理解しやすいと思う。

NumPyのFFT

FFTは多くの場合ライブラリで提供され、それを用いることになる。

自分で実装するのも楽しいものであるが、「高速」であることが大事なので、すでに最適化されたものを使用するのが楽である。

ここでは、PythonのNumPyライブラリに実装されているFFTを使用する。

https://numpy.org/doc/stable/reference/routines.fft.html

NumPyのFFTには以下の関数が含まれる。

Standard FFTs
- fft
- ifft
- fft2
- ifft2
- fftn
- ifftn
Real FFTs
- rfft
- irfft
- rfft2
- irfft2
- rfftn
- irfftn
Hermitian FFTs
- hfft
- ihfft
Helper routines
- fftfreq
- rfftfreq
- fftshift
- ifftshift

複素数信号を入力に取るようなfftと実数信号を入力に取るようなrfftがあり、またフーリエ逆変換を実行するifftとirfftがある。

また、2次元, n次元のバリアント、fft2, rfft2, ifft2, irfft2, fftn, rfftn, ifftn, irfftn, がある。

更に、複素数信号を入力に取るが入力信号にHermite対称性のあるような場合に使用できる、hfftと逆変換ihfftがある。

ヘルパールーチンのfftfreqとrfftfreqは、fft/rfftの結果得られる周波数領域のサンプルを求めるために使用する。

サンプリング周波数 $f_{s}$ の信号に対する、長さ $n$ (通常は2の累乗が用いられる)のfftは次のような周波数領域のサンプルを与える。

$f = {\frac{0}{n} f_{s}, \frac{1}{n} f_{s}, \frac{2}{n} f_{s}, \dots, \frac{\frac{n}{2} - 2}{n} f_{s}, \frac{\frac{n}{2} - 1}{n} f_{s}, - \frac{\frac{n}{2}}{n} f_{s}, - \frac{\frac{n}{2} - 1}{n} f_{s}, \dots, - \frac{1}{n} f_{s}}$

分母に注目すると、 $0$ から $\frac{n}{2} - 1$ まで1ずつ上がっていった後、 $- \frac{n}{2}$ となり、 $- 1$ まで1ずつ上がっていくという構造になっている。

これはビット数が $\log_{2} n$ の数値を $00. .0$ から $11. .1$ まで辞書順に並べて、2の補数表現の符号付き整数と解釈したのと同じである。

fftfreqはこのような配列を返すが、順序が整列されていないので、場合によっては面倒である。

そこでfftshiftというヘルパールーチンも用意されていて、これは、

$f = {- \frac{\frac{n}{2}}{n} f_{s}, \dots, - \frac{1}{n} f_{s}, \frac{0}{n} f_{s}, \frac{1}{n} f_{s}, \dots, \frac{\frac{n}{2} - 1}{n} f_{s}}$

と昇順に並び替えてくれる。ifftshiftはこの逆である。

複素数信号を入力に取る場合と、実数信号を入力に取る場合で異なる関数が使われるのは、実数信号の場合、fftの結果に対称性があって負の周波数部分は対応する正の周波数の複素共役となるため、計算をより高速にすることが可能だからである。

なぜ、実数信号の場合、fftの結果に対称性があるかというと、定義に戻って考えればわかる。

フーリエ変換の計算式

$X (ω) = \int_{- \infty}^{\infty} x (t) \exp [- i ω t] d t$

において両辺の共役を取ると、

$X^{*} (ω) = \int_{- \infty}^{\infty} x^{*} (t) \exp [- i ω t]^{*} d t = \int_{- \infty}^{\infty} x (t) \exp [i ω t] d t = X (- ω)$

これは、「負の周波数部分では対応する正の周波数の複素共役となる」ことを示す。

なお、この対称性は、Hermite対称性と呼ばれる。

実用上、多くの場合実数信号が扱われる。今回のデータに対してもrfftを使用する。

rfftfreqは次のような配列を返す。

$f = {\frac{0}{n} f_{s}, \frac{1}{n} f_{s}, \frac{2}{n} f_{s}, \dots, \frac{\frac{n}{2} - 1}{n} f_{s}, \frac{\frac{n}{2}}{n} f_{s}}$

コードとしては以下と同じである。

import numpy as np

def my_rfftfreq(n, fs):
    return np.linspace(0, fs / 2, n // 2 + 1)

なお、numpy.fft.rfftfreqはサンプリング周波数 $f_{s}$ を受け取るのではなく、その逆数であるサンプリング間隔 $d = \frac{1}{f_{s}}$ を受け取るようになっていることには注意されたい。

rfftの場合、もともと昇順にソートされているので、rfftshiftのような関数は必要ない。

rfftfreqの結果の最後の要素は、 $\frac{f_{s}}{2}$ であるが、これはナイキスト周波数と呼ばれている。

標本化定理によると、ナイキスト周波数は与えられたサンプリング周波数で復元できる信号の周波数の上限である。

音声データ1 : 440Hz正弦波

音声データの1つ目は, 440Hzの正弦波が10秒間続くデータである。音高(pitch)としては、ラ(A4)の音に当たる。

この音声は次のコードで作成した。

import numpy as np
import scipy.io.wavfile as wavfile

# パラメータ設定
fs = 48000  # サンプルレート（Hz）
f = 440.0  # 正弦波の周波数（Hz）
duration = 10.0  # 正弦波の長さ（秒）

n_samples = int(fs * duration)

# 時間軸の作成
t = np.linspace(0, duration, n_samples, endpoint=False)

# 正弦波の生成
s = np.sin(2 * np.pi * f * t)

# 音声信号を16ビットPCM形式に変換
s_16bit_pcm = np.int16(s * 32767)

# WAVファイルの書き出し
wavfile.write("sine_wave.wav", fs, s_16bit_pcm)

この信号の最初の4096サンプルをプロットすると次のようになる。

さて、この信号をFFTしてみよう。

先程のコードに引き続いて、FFTを実行する。

# 最初の4096サンプルを取り出し
s = s[:4096]

# FFT
z = np.fft.rfft(s)

# 周波数
f = np.fft.rfftfreq(len(s), 1 / fs)

fを横軸に、zの絶対値を縦軸に取ると、周波数領域のプロットとなる。

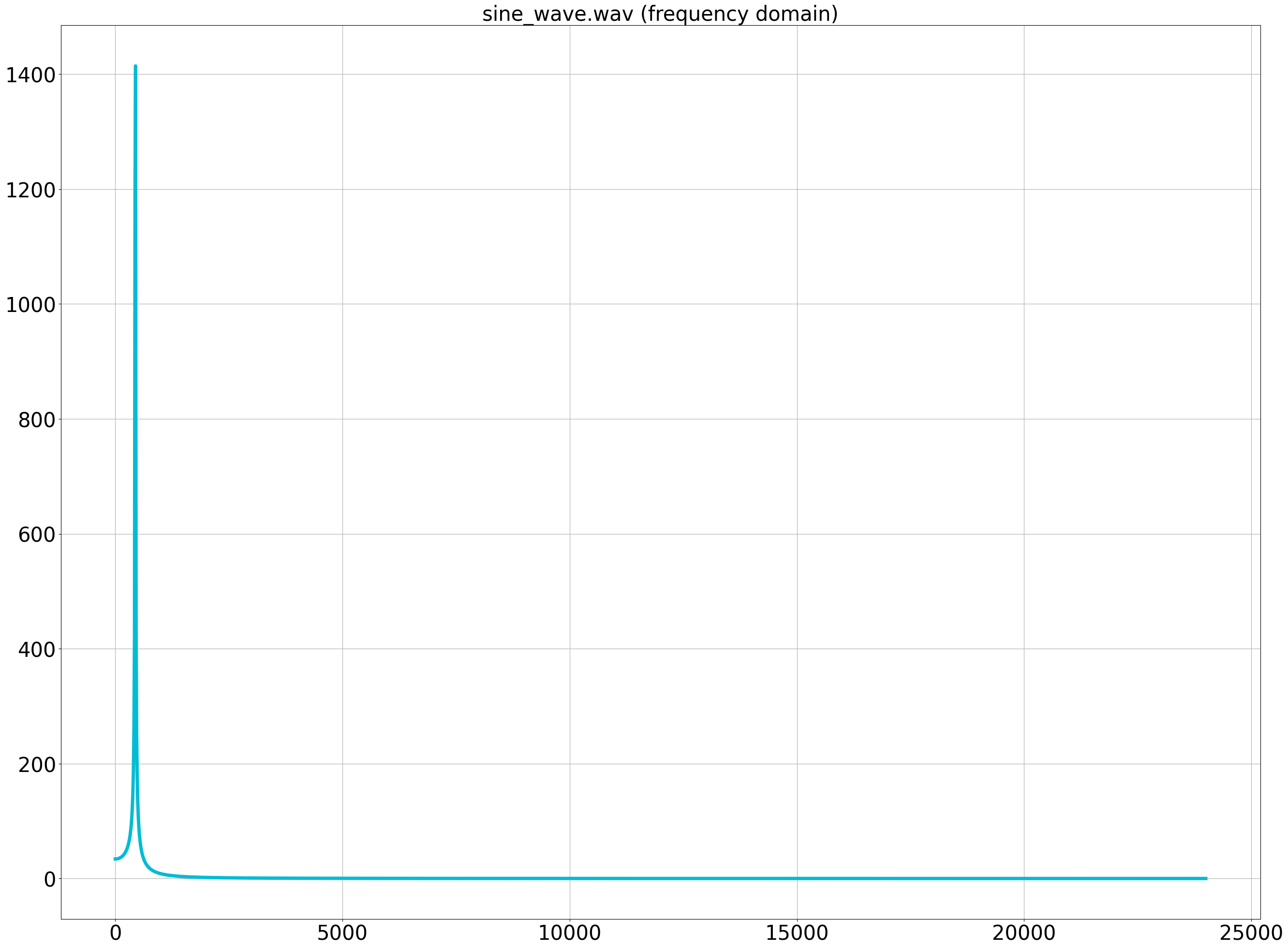
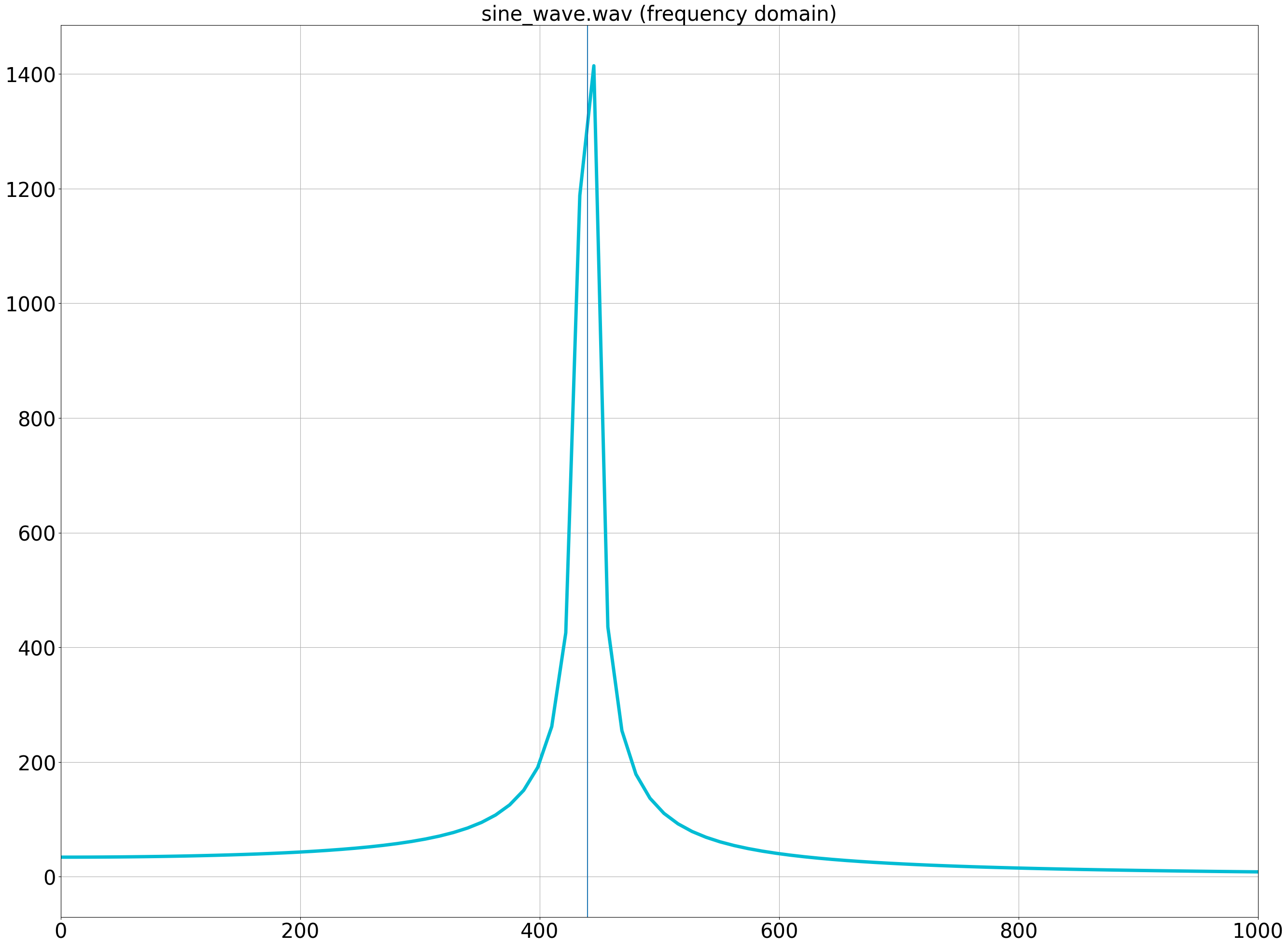
440Hz付近を拡大すると、入力信号の440Hz付近にピークが立っていることが確認できる。

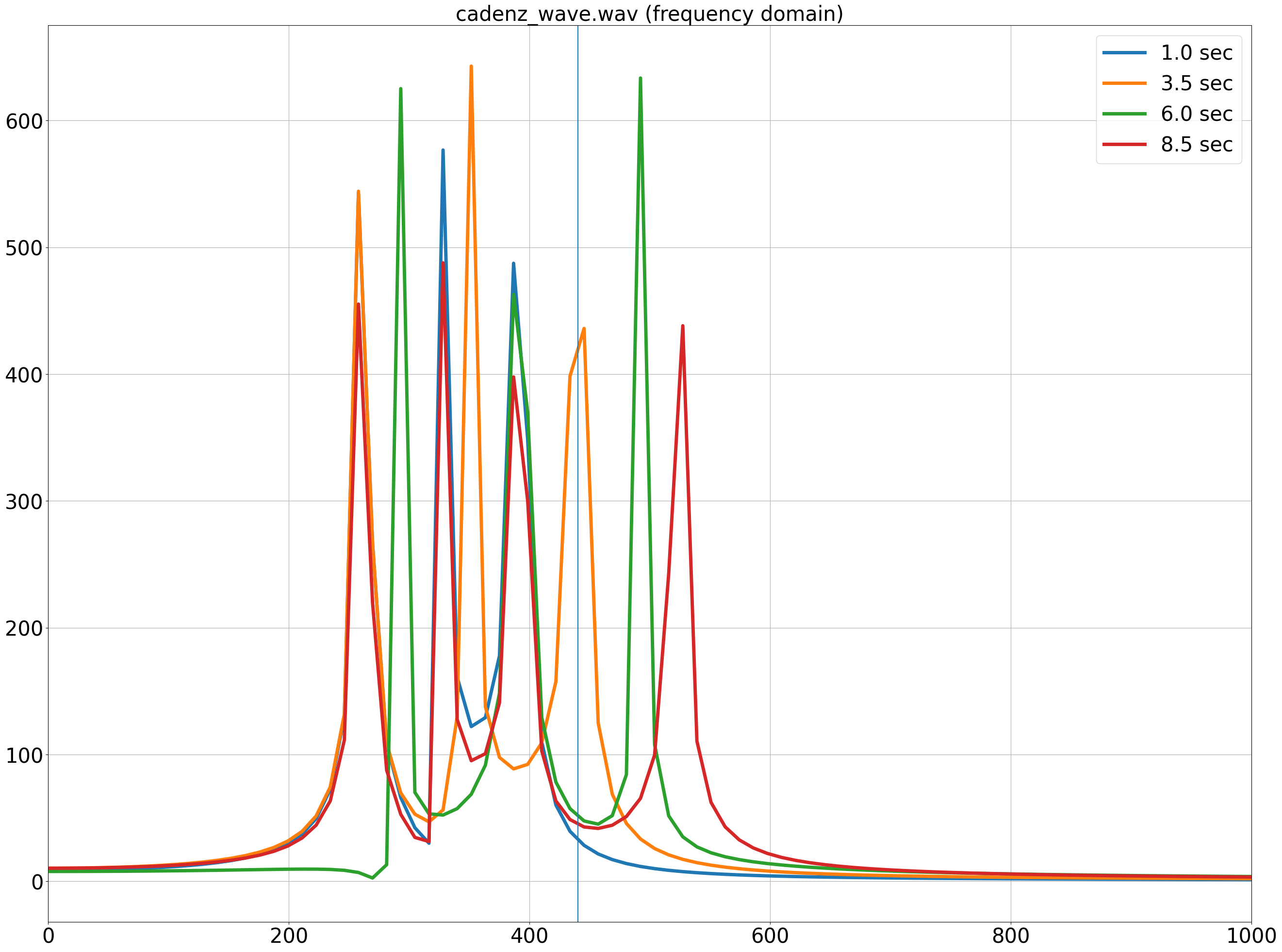
音声データ2 : C-F-G-Cカデンツ

音声データの2つ目はC-F-G-Cカデンツである。

音声データ1と異なる点は2つある。

複数の周波数の音が混ざり合って和音を形成していること
和音が時系列で変化すること

である。

1秒時点、3.5秒時点、6秒時点、8.5秒時点のそれぞれで、長さ4096のFFTを実行した結果は次の図のとおりである。

それぞれの時点で3つもしくは4つのピークが見え、和音の構成音に対応していることがわかる。

また、それぞれのそれぞれの時点で、ピークの位置が異なっていることから、時系列で音が変化していることもわかる。

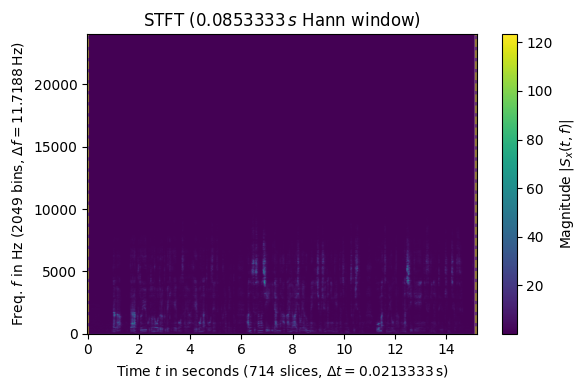
スペクトログラム

音声データ2でみたように、時系列で音が変わっていくのは、とても普通のことである。

普段聞いている音楽も、時系列で周波数が変化していくことによってメロディーが生まれ、そこに面白みがある。

上の図のように、各時点でのFFTの結果を色を変えながらグラフに表すこともできるが、時系列の変化を追うという意味では分かりづらい。

そこで、横軸に時間、縦軸に周波数を取り、それぞれの交点に強度を表す色付けをするようなグラフが考案されている。

このような図をスペクトログラムといい、音響分野では広く使われている。

SciPyのSTFT

スペクトログラムを描くには、短時間フーリエ変換(STFT)を実行する。

短時間フーリエ変換は、簡単に言えば入力信号を細かいチャンク(短時間)に分割して、それぞれのチャンクでフーリエ変換を行うことである。

実際には、窓関数と呼ばれる(一般的には山形の)関数をかけることで注目している時間を明瞭にし、またチャンク同士をオーバーラップさせることで周波数の変化ができるだけ滑らかになるように実装する。

ここでは、SciPyのsignalモジュールに含まれるShortTimeFFTクラスを使用する。

https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.ShortTimeFFT.html#scipy.signal.ShortTimeFFT

scipy.signal.windowsにさまざまな窓関数が定義されているが、今回はハン窓(hann window)を使用する。最もよく使われる窓関数である。

また、オーバーラップ幅はチャンク幅の3/4とする(つまり、hopは1/4である)。

短時間フーリエ変換の実行は次のようになる。

# ハン窓
win = signal.windows.hann(4096)

# 短時間フーリエ変換
SFT = signal.ShortTimeFFT(win, 4096 * 1 // 4, fs)
Sx = SFT.stft(s)

リファレンスの例に従って描いたスペクトログラムが下図である。

0.0s - 2.5s : ド・ミ・ソ
2.5s - 5.0s : ド・ファ・ラ
5.0s - 7.5s : レ・ソ・シ
7.5s - 10.0s : ド・ミ・ソ・ド

となっていることが見て取れる。

音声データ3 : 朗読

最後に、人間の声のスペクトログラムの例として、私の朗読音声をスペクトログラム化したものを示す。

成人男性の地声はおおよそ120Hz - 200Hz程度であると言われており、スペクトログラムにピークがあることとも一致する。

一方で、7000Hz程度の高い周波数も音声に含まれていることもわかる。

特に、6.5秒付近と12.5秒付近では5000Hz付近に際立ったピークがある。

元の音声を聞いてみると、この部分はサ行のシビラント(歯擦音)が強く発生している箇所のようである。