Simulation of the Monty Hall Problem
What is the Monty Hall Problem?
The Monty Hall Problem is known as a probability puzzle that yields results contrary to intuition.
It is based on the American television show “Let’s Make a Deal.”
The problem became widely known after being published in a magazine in 1990 although the problem itself predates this publication.
The problem as stated in that publication is as follows:
Suppose you’re on a game show, and you’re given the choice of three doors:
Behind one door is a car; behind the others, goats.
You pick a door, say No. 1, and the host, who knows what’s behind the doors, opens another door, say No. 3, which has a goat.
He then says to you, “Do you want to pick door No. 2?”
Is it to your advantage to switch your choice?
The answer is “Yes, switching is advantageous.”
This answer contradicted the intuition of many people, leading to considerable debate.
In this article, instead of providing a detailed explanation of the Monty Hall problem’s answer (because it is already explained in great detail on many other websites), we will verify this result through simulation.
Overview of the Simulation
We will consider three different strategies for players and run the game 10,000 times for each strategy.
We will plot the changes in win rates up to 10,000 trials.
1. Stubborn Player
The Stubborn Player never changes their initial choice even after a goat door is revealed.
2. Capricious Player
The Capricious Player randomly decides whether or not to switch their choice after a goat door is revealed.
3. Flexible Player
The Flexible Player always switches to a different door after a goat door is revealed.
Simulation Results
The results of the simulation are as follows:
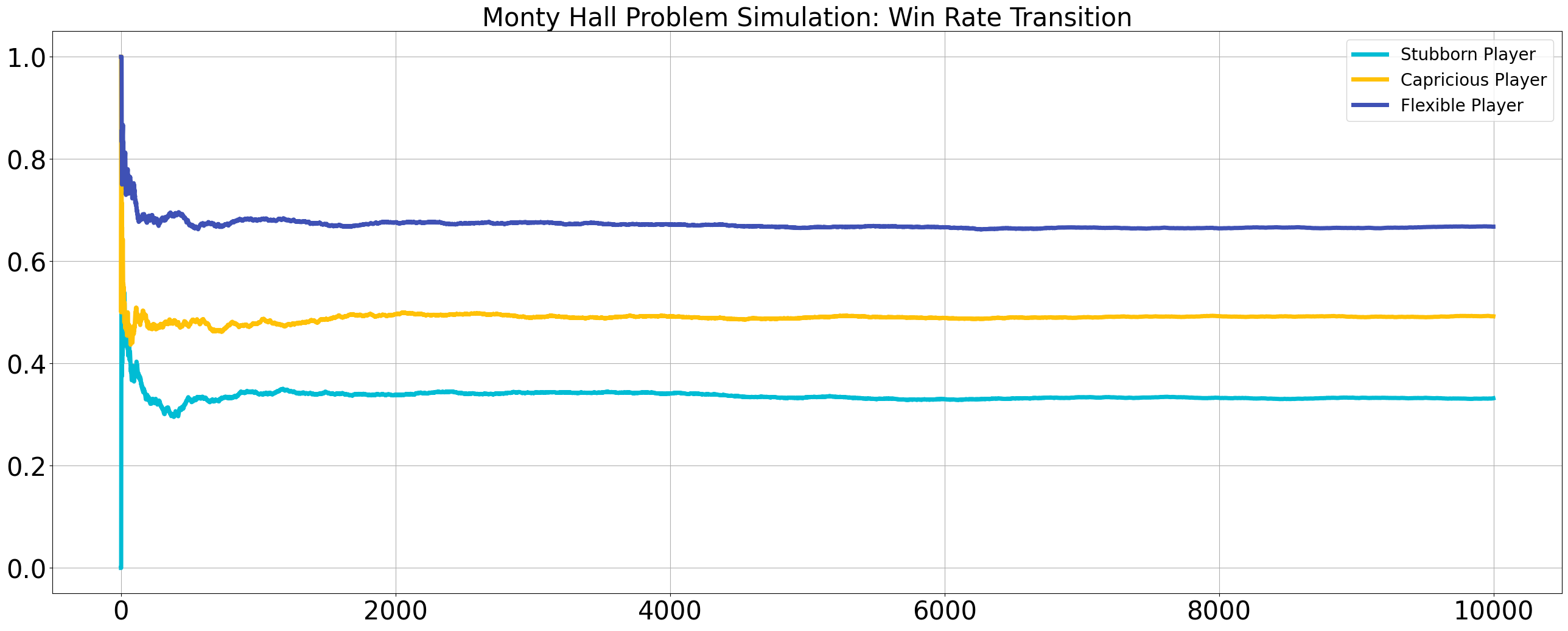
Focusing on the results after 10,000 trials:
- The Stubborn Player has the lowest win rate, approximately
- In contrast, the Flexible Player has the highest win rate, approximately
- The Capricious Player falls in between, with a win rate of approximately
This is consistent with the calculations.
Simulation Code
Below is the simulation code written in Python.
By examining the simulation code, you can understand the cause of the counterintuitive results (the key point is the open() method in the MontyHall class).
#! /usr/bin/env python
import abc
from dataclasses import dataclass
from random import choice, randint
import numpy as np
from matplotlib import pyplot as plt
@dataclass
class Player(abc.ABC):
"""Abstract base class for players"""
selected: None | int = None
"""Stores the previous choice"""
def __init__(self):
pass
def select(self) -> int:
"""Initial choice"""
self.selected = randint(1, 3)
return self.selected
@abc.abstractmethod
def reselect(self, opened: int) -> int:
"""Reselect after being shown a goat
To be implemented in concrete classes
"""
pass
class StubbornPlayer(Player):
"""Player who sticks to the initial choice even after a goat is revealed"""
def reselect(self, opened: int) -> int:
if self.selected is None:
raise ValueError("Not selected yet")
return self.selected
class CapriciousPlayer(Player):
"""Player who randomly decides to switch or not after a goat is revealed"""
def reselect(self, opened: int) -> int:
if self.selected is None:
raise ValueError("Not selected yet")
s = {1, 2, 3} - {opened}
return choice(list(s))
class FlexiblePlayer(Player):
"""Player who always switches to a different door after a goat is revealed"""
def reselect(self, opened: int) -> int:
if self.selected is None:
raise ValueError("Not selected yet")
s = {1, 2, 3} - {self.selected, opened}
assert len(s) == 1
return s.pop()
@dataclass
class MontyHall:
"""Game master: Monty Hall"""
answer: int
"""Monty Hall knows the answer"""
def __init__(self) -> None:
self.answer = randint(1, 3)
def open(self, selected: int) -> int:
"""Reveal a goat behind one of the doors not selected"""
s = {1, 2, 3} - {self.answer, selected}
return choice(list(s))
def check_the_answer(self, selected: int) -> bool:
"""Check the answer
return: True if correct, False if incorrect
"""
return selected == self.answer
def game(player: Player, monty_hall: MontyHall):
"""Conduct the game"""
selected = player.select()
opened = monty_hall.open(selected)
selected = player.reselect(opened)
if monty_hall.check_the_answer(selected):
print("Win!")
return True
else:
print("Lose...")
return False
def win_rates(results: list[bool]) -> np.ndarray:
"""Calculate the win rate progression"""
r = np.asarray(results)
return np.cumsum(r) / np.arange(1, len(r) + 1)
def main():
stu_results = []
for _ in range(10000):
result = game(StubbornPlayer(), MontyHall())
stu_results.append(result)
cap_results = []
for _ in range(10000):
result = game(CapriciousPlayer(), MontyHall())
cap_results.append(result)
flex_results = []
for _ in range(10000):
result = game(FlexiblePlayer(), MontyHall())
flex_results.append(result)
plt.rcParams["figure.figsize"] = (32.0, 12.0)
plt.plot(win_rates(stu_results), label="Stubborn Player", color="#00BCD4", lw=5)
plt.plot(win_rates(cap_results), label="Capricious Player", color="#FFC107", lw=5)
plt.plot(win_rates(flex_results), label="Flexible Player", color="#3F51B5", lw=5)
plt.title("Monty Hall Problem Simulation: Win Rate Transition", fontsize=30)
plt.legend(fontsize=20)
plt.xticks(fontsize=30)
plt.yticks(fontsize=30)
plt.grid()
plt.savefig("monty_hall_sim.png", bbox_inches="tight", transparent=True)
if __name__ == "__main__":
main()