Implemented k-means in C++
What is k-means?
The k-means algorithm is arguably the most well-known clustering algorithm.
It takes a set of points as input and divides them into k clusters.
The value k must be specified beforehand.
This division is performed based on the distances (or proximity) between the points.
In machine learning, the term “classification” is also used, which might be confusing.
However, classification involves learning from a large number of labeled data points to predict the labels of new, unlabeled data.
Classification is supervised learning, while clustering is unsupervised learning.
Although k-means has the significant drawback of requiring the number of clusters to be predefined, its simplicity makes it effective in certain situations.
Repository
I implemented k-means in C++ and stored the code in the following repository:
https://github.com/hokacci/cluster/tree/main
The implementation is kept simple to illustrate the functionality of k-means, though it may not be ideal for practical use.
This article explains the code implemented in the repository.
Repository Structure
The repository is organized as follows:
The include/kmeans.h file contains the templated implementation of k-means, while example/example_kmeans_blobs_2d.cpp is a sample code that utilizes it.
.
├── example
│ ├── example_kmeans_blobs_2d.cpp
│ └── helpers
│ ├── include
│ │ ├── blobs_2d.h
│ │ └── point_2d.h
│ └── src
│ ├── blobs_2d.cpp
│ └── point_2d.cpp
└── include
└── kmeans.h
Concept of k-means
Using the concept feature introduced in C++20, constraints for the space in which the data points belong are defined as follows:
// Concept for points used in k-means
template <typename Point>
concept KMeansablePoint = requires(Point a, Point b, std::vector<Point> points) {
// A function to calculate the distance between two points must be defined
{ distance(a, b) } -> std::convertible_to<double>;
// A function to calculate the centroid of points must be defined
{ center(points) } -> std::convertible_to<Point>;
};
In k-Means, two operations are required:
- Measuring the distance between two points.
- Calculating the centroid of multiple points.
While these two operations are naturally defined in ordinary Euclidean space, defining them as a concept makes the key points of k-Means explicit.
As the name suggests, computing the “mean,” or centroid, is the core of the algorithm.
It highlights that simply having a notion of distance is insufficient.
Overview of k-means Flow
The k-means implementation constrains the template parameter Point using the previously defined concept.
The flow of k-means is described in the exec() member function:
template <KMeansablePoint Point>
struct KMeans
{
...
// Execute k-means
void exec()
{
init_centroids();
update_labels();
for (int i = 0; i < max_iter; ++i)
{
update_centroids();
bool updated = update_labels();
if (!updated)
{
break;
}
}
}
...
};
The algorithm begins by randomly selecting k centroids using init_centroids().
Next, update_labels() assigns a label to each point based on the nearest centroid.
Then, update_centroids() updates the centroids by calculating the centroid of points with the same label.
These steps are repeated until no labels change or the maximum number of iterations is reached.
The process is simple and straightforward.
Note that in update_labels(), the distance() function defined in the concept is called.
Similarly, the center() function is invoked in update_centroids().
Example Implementation (2D Data)
An example of executing k-means with 2D data is implemented in example/example_kmeans_blobs_2d.cpp.
The Point2D structure and the associated distance() and center() functions are defined as follows:
// Struct representing a 2D point
struct Point2D
{
double x = 0;
double y = 0;
};
// Compute the distance between two points
double distance(const Point2D &a, const Point2D &b)
{
return std::sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
// Compute the centroid
Point2D center(const std::vector<Point2D> &points)
{
Point2D c;
for (auto p : points)
{
c.x += p.x;
c.y += p.y;
}
c.x /= points.size();
c.y /= points.size();
return c;
}
Here, distance() measures the Euclidean distance using the Pythagorean theorem,
and center() simply calculates the vector average.
There should be no issues with these implementations.
The sample dataset for Point2D is defined as std::vector<Point2D> dataset_blobs_2d in blobs_2d.(h|cpp).
This dataset is derived from the toy dataset commonly used in Python’s scikit-learn library.
Example Implementation (Visualization)
Visualization is implemented in example/example_kmeans_blobs_2d.cpp using matplot++, a library similar to Python’s matplotlib.
Points are colored based on their labels, and centroids are displayed as cross marks.
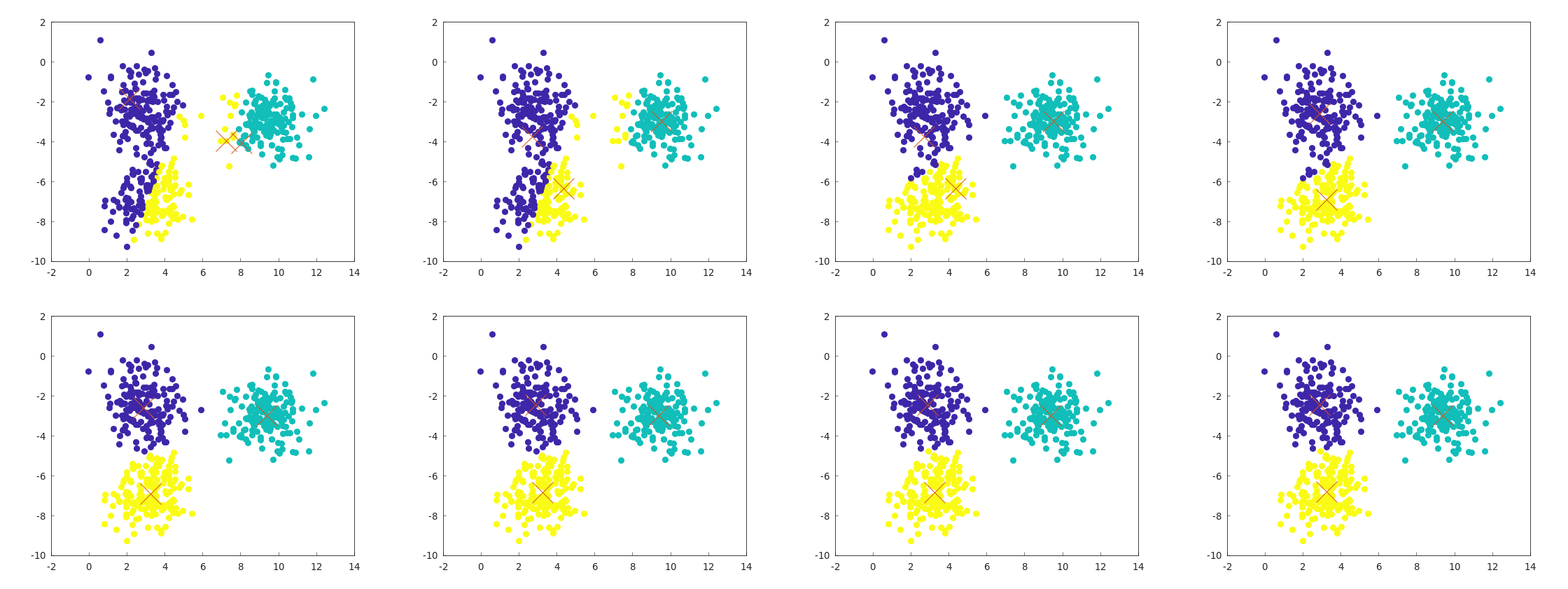
Example Behavior of k-means
Below is an example of the behavior of example_kmeans_blobs_2d.cpp.
The flow starts at the top-left and ends at the bottom-right, showing the alternation between centroid updates and label updates.
Failure Case of k-means
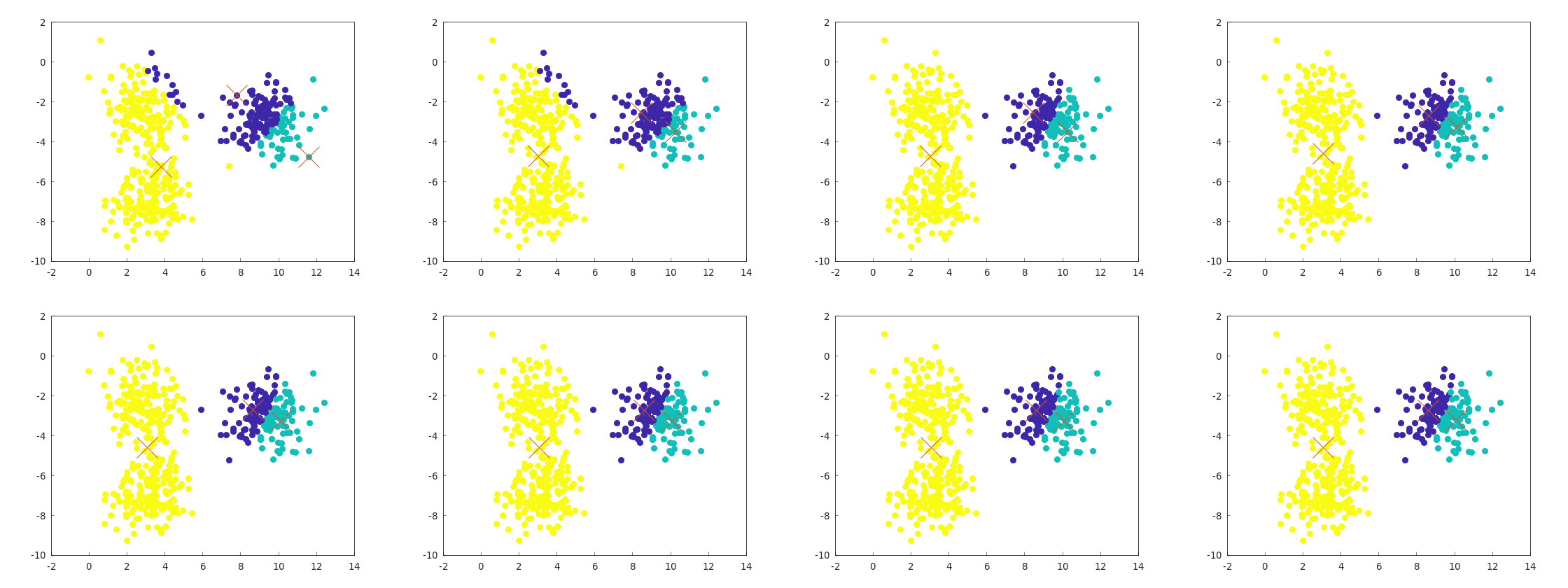
A major drawback of k-means is its susceptibility to local minima.
Below is an example of a failure case caused by poor initial centroid selection:
k-means++
An improved version of k-means, called k-means++, refines the initial centroid selection process.
I may try implementing k-means++ and other clustering algorithms in the future.